search

	Home > Balistica > Sottomenu > Documento	back

La teoria della rosata

Le nozioni di balistica esterna necessarie per calcolare la traiettoria dei pallini da caccia sono esposte nel precedente capitolo. Qui cercheremo di esporre le nozioni basilari sulla rosata e sulla efficacia venatoria dei pallini. Non ci occuperemo delle munizioni per tiro al piattello.
I pallini sono prodotti con una lega di piombo indurita da antimonio, con un peso specifico medio di circa 11,1 gr/cm³. Vi sono in commercio anche pallini di acciaio, ma non sono di rilevante interesse venatorio.
A seconda delle esigenze venatorie si usano pallini di vario diametro, con i seguenti dati.

Tabella con misure di vari pallini

Si tenga presente che nei vari paesi esistono poi numerazioni convenzionali e che ad ogni numero non corrisponde ad una frazione tonda di millimetro; in Italia, ad esempio,una delle numerazioni usuali è la seguente; possono però esservi variazioni rispetto ad altre tabelle. Il numero 2/0 si legge "due zeri".

I pallini superiori ad un certo diametro vengono chiamati volgarmente "pallettoni", ma non vi è un criterio uniforme su dove porre la linea di distinzione. In alcuni paesi (Germania, Inghilterra, USA) si usa una denominazione particolare per pallini con diametro superiore a 6 mm, in altri oltre i 5 mm, in Italia invece solo per pallini la cui numerazione è indicata in zeri. Non è comunque distinzione che abbia un qualsivoglia fondamento giuridico poiché per la legge si deve solo distinguere fra munizione spezzata e munizione a palla unica.

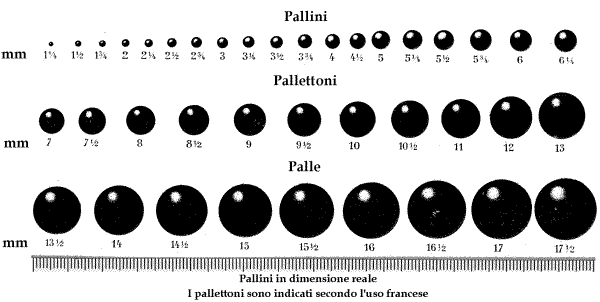
I pallini vengono sparati da canne cilindriche o da canne conformate con particolari modelli e misure di restringimento degli ultimi centimetri di volata, detti strozzature.
I pallini che escono da una canna cilindrica tendono ad allargarsi radialmente perché la resistenza dell'aria ha all'inizio maggior presa sugli strati esterni dello sciame di pallini che non su quelli al centro. Inoltre il borraggio può avere inizialmente una velocità superiore a quella dello sciame e "bucarne" la parte centrale.
La funzione della strozzatura è di evitare questi inconvenienti.

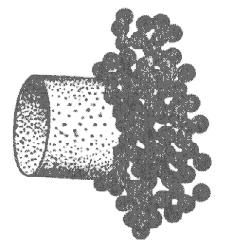
Disposizione dei pallini e borra, sparati con canna cilindrica, a 1,2 metri dalla volata

Pallini e borra, sparati da canna molto strozzata, a 1,2 metri dalla volata

I pallini dello strato esterno vengono compressi e rallentati per il maggior attrito e comprimono il gruppo al centro che acquista maggior velocità e li sorpassa; la borra viene frenata e rimane indietro. Inoltre i pallini esterni vengono assoggettati ad una forza che li dirige verso l'asse della canna e compensa quindi la loro tendenza ad allargarsi radialmente; solo i pallini che si sono molto deformati per l'attrito contro le pareti della canna sfuggono a questo recupero. Il risultato è che lo sciame di pallini si allunga un po' di più rispetto a quello sparato dalla canna cilindrica, ma però un maggior numero di pallini viene indirizzato a viaggiare parallelamente all'asse delle canna. Perciò la dispersione radiale inizia più tardi quando la resistenza dell'aria riesce ad agire all'interno dello sciame, in modo diverso sui singoli pallini (punto di apertura).
L'effetto della strozzatura sulla velocità dei pallini è del tutto trascurabile.
Lo scopo della strozzatura non è quello di concentrare al massimo la rosata di pallini, ma quello di avere, alla distanza voluta, la copertura ottimale della rosata che deve avere una certa dimensione per garantire che il bersaglio venga colpito senza troppa difficoltà, ma da un numero di pallini sufficiente ad ucciderlo.
Come si è detto i singoli pallini acquistano velocità e direzioni diverse per effetto delle variazioni di forma entro la canna, e conseguente spostamento del centro di gravità, per le diverse forze a cui vengono assoggettati dalla strozzatura, per gli urti reciproci entro la canna e fuori di essa; la strozzatura allunga lo sciame e perciò diminuiscono le probabilità che pallini arretrati, ma di forma migliore, raggiungano pallini anteriori deformati e che entrambi rimbalzino fuori dello sciame. Si consideri che il 10-15% dei pallini è fortemente deformato e che almeno un terzo dei pallini ha qualche deformazione (pallini da 2 mm; la percentuale sale fino al 65% per pallini da 4 mm).
I pallini poi non viaggiano sempre in modo rettilineo, ma, come ogni altro proiettile, con deviazioni spiraliformi attorno alla linea di traiettoria: se si spara a 20 metri ad un bersaglio la cui metà sinistra è imperforabile, si vede che a 40 metri la metà sinistra di un secondo bersaglio viene egualmente colpita da pallini che a 20 metri si trovavano necessariamente sul lato destro.
Le dimensioni e la distribuzione della rosata vengono rilevate con un bersaglio posto ad una data distanza e, salvo alcuni pallini anomali, la sua forma è pressoché circolare; la distribuzione dei pallini entro questo cerchio è alquanto imprevedibile, ma è evidente che in una buona rosta la densità deve essere maggiore al centro che non ai margini. Avviene così che un corpo avente la superficie frontale di 90 cm² (corrispondente ad una pernice), viene colpito da numerosi pallini se si trova al centro della rosata e da un minor numero di pallini se si trova spostato verso il suo margine. Siccome il selvatico deve essere colpito da più pallini, si avrà una buona rosata quanto più uniformemente i pallini sono distribuiti all'interno del cerchio, così che in ogni suo punto il selvatico abbia le stesse probabilità di essere colpito dal numero di pallini richiesto, visto che non è facile coglierlo proprio al centro della rosata!
A breve distanza si avrà una rosata piccola e con troppi pallini. Poi la rosata e la dispersione dei pallini aumentano con la distanza finché alla distanza ottimale di tiro, per una data carica, si avrà la distribuzione dei pallini migliore; aumentando ancora la distanza, aumenta la rosata, ma si restringe via via la zona centrale in cui è garantita la densità richiesta dei pallini.
La velocità iniziale dei pallini ai fini degli studi di balistica viene convenzionalmente assunta come pari a 360 ms, anche in considerazione del fatto che qualche decina di ms in più o in meno alla bocca, diventano poi pochi ms alle distanze venatorie e del fatto che questa risulta essere la velocità ottimale sotto molti punti di vista. Una velocità superiore richiede notevole aumento delle pressioni con un peggioramento della rosata non accompagnato da alcun vantaggio alla maggior distanza raggiungibile. Una velocità inferiore aumenta di molto la bontà della rosata, ma diminuisce troppo la penetrazione del pallino. Se un fucile dà una buona rosata solo con cariche deboli, non è buon fucile.
Nei primi metri di traiettoria non è poi possibile determinare la velocità dei singoli pallini in quanto la carica si comporta aerodinamicamente come un proiettile e ogni pallino inizia ad avere una traiettoria autonoma solo quanto è esposto alla resistenza dell'aria con esclusione degli influssi reciproci con gli altri pallini. La distanza a cui ciò avviene dipende dalla velocità iniziale, dal diametro del pallino, dal tipo e grado di strozzatura e dalla deformazione subita dai pallini.
Il Burrard (studioso inglese) assume come distanza minima quella di 3 yarde (m. 2,75) e misura a partire da essa la velocità iniziale dei pallini. In Germania si usa misurare la velocità a 5 m dalla bocca, distanza a cui con sicurezza ogni pallino viaggia per conto suo e si riscontra che se essa è pari a 360 ms, la velocità alla bocca può variare da 385 a 395 ms a seconda di misura dei pallini, calibro, peso della carica.
Ecco la perdita di velocità dei pallini alle varie distanze:

Tabella della perdita di velocità di un pallino di dato diametro a varie distanze,
posto che la velocità a 5 metri dalla volata sia eguale a 360 m/s:

Tabella del tempo impiegato a percorre varie distanze
posto che la velocità a 5 metri dalla volata sia eguale a 360 m/s

La curvatura della traiettoria dei pallini può essere trascurata perché ampiamente compensata dalle dimensioni della rosata così da non richiedere compensazioni al momento della mira. Un pallino di 2,5 mm cade di 1,9 cm a 20 m, di 5,5 a 30, di 12,3 a 40 metri; un pallino di 3,5 mm cade di 1,8 a 20 m ,di 4,9 a 30, di 10,3 a 40 e di 19,3 a 50 metri. I fucili del resto sono tarati a 35 metri di distanza e a 10-15 cm sopra il centro ideale della rosata così che lo scarto massimo effettivo non supera i 10-15 cm.
Come detto, mentre la rosata sul bersaglio viene rappresentata come un cerchio, in effetti i pallini formano uno sciame allungato con una maggior presenza di pallini nella parte anteriore; se si divide lo sciame in due parti contenente lo stesso numero di pallini, si constata che il punto di divisione (centro di gravità dello sciame) si trova ad 1/3 dai pallini di testa.
Sperimentalmente non si rilevano significative influenze della temperatura, dell'umidità dell'aria, dell'altitudine, sulla velocità iniziale e sulla traiettoria, anche se i cacciatori usano aumentare le cariche in inverno (ma in inverno gli animali sono più protetti da piume e pelo).
Maggiore e significativa può essere l'influenza del vento laterale, specialmente se si spara in aria (a terra il vento e minore e vi è la protezione di piante e cespugli). Con un vento di 5 m/s un pallino di 2,5 mm viene spostato di 10 cm a 25 m, di 20 cm a 35, di 35 cm a 45 m. (le deviazioni si raddoppiano se il vento soffia a 10 ms). Bisogna però tenere presente che nel tiro a volo anche il selvatico viene spostato nella stessa direzione dei pallini.

La carica di pallini
Il peso della carica di pallini per un dato calibro non può variare di molto: una carica troppo pesante aumenta la pressione dei gas ed aumenta il rinculo; se l'arma è pesante si può usare una carica maggiore perché il rinculo sarà minore; un'arma leggera richiede una carica leggera per non avere un rinculo poco piacevole. La carica normale per un cal. 12/70 è di 35-36 gr, per un 16/70 di 30-31 gr, per un 20/70 di 26-27 gr. In cartucce maggiorante (Magnum, Super speed) si può però arrivare fino a cariche di 46 grammi per il calibro 12.
Quando si usano pallini di grosse dimensioni, il peso della carica può essere aumentato un poco, senza che si verifichi un aumento di pressione perché con più i pallini sono grossi minore è l'attrito fra i singoli pallini. Il problema dell'attrito è ora divenuto secondario per l'uso di borre di plastica che racchiudono il pallino fino all'uscita dalla canna.

L'aumento di diametro della rosata
In molti testi si legge che l'aumento della rosata non sarebbe proporzionale alla distanza dall'arma, ma un po' minore. Ciò ovviamente non può avvenire, in contrasto con le leggi della fisica. I pallini hanno un comportamento diverso nei primi 10-12- metri di percorso rispetto al tratto successivo e se si prende in esame l'intera traiettoria, effettivamente si riscontra la non linearità dell'allargamento. Se però si stabilisce la dispersione a 35 metri, la dispersione a 25 metri o a 45 metri non potrà che essere proporzionale alla distanza. Ciò non è accertabile con precisione assoluta per il fatto che i pallini, come si è detto, procedono con un moto spiraliforme e di conseguenza la distribuzione sul bersaglio in un dato istante finisce per essere casuale e non predeterminabile. Inoltre una misurazione esatta richiede un bersaglio molto ampio che consenta di visualizzare tutti i pallini; la valutazione cambia infine notevolmente a seconda che si consideri l'intera rosata oppure solo la sua parte centrale. Si ripete perciò è fonte di errore (ad esempio) valutare le dimensioni della rosata a 40 metri in base alla rosata misurata a 10 metri.
L'aumento della dispersione è maggiore per i pallini piccoli che per i pallini grossi.
Quelli piccoli iniziano a disperdersi più vicini all'arma e si deformano più facilmente dei pallini grossi. Se si prendono in considerazione tutti i pallini della rosata, anche i più esterni, si riscontra così che la dispersione dei pallini di 2,5 mm può essere superiore del 50% a quelle dei pallini di 3,5 mm. Se si prende in considerazione solo la parte centrale della rosata, in cui si trovano i 5/6 dei pallini si ha una dispersione superiore solo del 10-25 %. Lo stesso fenomeno non si riscontra più con pallini di 4 mm! Va detto però che ogni strozzatura provoca una diversa dispersione così che ha poco senso cercare di elaborare una teoria generale.
In linea molto approssimativa si può ritenere che se su di un bersaglio di dimensioni qualsiasi, alla distanza di 35 metri si contano 100 pallini, alle diverse distanze si abbia il seguente numero di pallini:

Bisogna quindi fare molto attenzione alle canne troppo strozzate perché oltre la distanza per cui si cerca di avere la concentrazione ottimale, la dispersione della rosata può poi aumentare in modo da essere del tutto insufficiente.
Per valutare molto approssimativamente le dimensioni dell'intera rosata alle varie distanze, si può fare ricorso alla tabella elaborata da M. Baker. Le dimensioni sono in pollici.

Le dimensioni della rosata non sono correlabili al calibro dell'arma; in piccoli calibri si riscontra sovente un maggior numero di pallini con traiettoria anomala.
Si ripete comunque che è impossibile dare indicazioni che non siano approssimative. Fucili aventi canne con identiche dimensioni interne e strozzatura identica al centesimo di millimetro, hanno prestazioni differenti e basta la cromatura delle canna per modificarle.
Una approssimativa valutazione delle dimensioni della rosta alle gittata massima dei pallini è importante per valutare il rischio di persone che si trovino a quella distanza e in quella direzione. Esperimenti svolti in Germania hanno dato i seguenti risultati

Ciò significa che se si spara verso un selvatico con pallini di 2,5 mm e dietro di esso, a 180 metri di distanza, vi è una persona, questa può essere colpita anche se si trova spostata di 40 metri rispetto alla linea di tiro! Questo senza tenere conto di possibili rimbalzi, di deviazioni anomale, di cartucce con dispersore (che danno a 20 metri il bersaglio che altrimenti si avrebbe a 35 m), di strozzatura per skeet, ecc..
Secondo le norme di prudenza elaborate in Germania, quando si caccia con altre persone, non si dovrebbe sparare verso di loro sotto un angolo minore di 10 gradi; ciò significa che a 40 metri di distanza il compagno deve trovarsi almeno a 7 metri dalla lepre (a 20 gradi e a 14 metri se si usa un dispersore). Non sarebbe male che ogni cacciatore si abituasse a valutare istintivamente questo angolo.

La lunghezza della rosata
La lunghezza della rosata non deve essere confusa con la lunghezza dello sciame di pallini in volo.
Se si spara su di uno specchio d'acqua, verso un anatra ad una trentina di metri, è facile constatare a vista che i pallini colpiscono una striscia di acqua lunga più di 10 metri. Questa striscia non deriva dal fatto che lo sciame di pallini assume una forma allungata, ma da un normale fenomeno balistico. Se a 35 metri l'intera rosata ha un diametro di circa un metro, vuol dire che alcun pallini si troveranno al livello dell'acqua ed altri ad mezzo metro circa da essa, alcuni più veloci, altri più lenti; percorrono perciò traiettorie diverse e i pallini più lenti o più bassi colpiranno l'acqua circa 20 metri prima dell'anatra, quelli più alti e più veloci a circa 20 metri dopo l'anatra (dati puramente esemplificativi, ovviamente); la conseguenza è una lunga strisciata di pallini sull'acqua e una differenza di tempo di volo tra pallini anteriori e pallini posteriori di 0,2- 0,3 secondi. Ciò non significa ovviamente che non sia importante mirare bene un selvatico che fugge davanti a noi in linea retta perché comunque la concentrazione richiesta di pallini si ha solo attorno al punto mirato.

La lunghezza dello sciame di pallini
Il problema delle dimensioni e disposizione dello sciame di pallini lungo la traiettoria, è stata oggetto di numerosi studi i quali, in fin dei conti, hanno concluso che è un problema di scarso interesse. In modo abbastanza indipendente da carica e da strozzatura, i pallini si allungano in uno sciame a forma di grappolo d'uva, con la parte più ampia in avanti e che a 35 metri di distanza è lungo 3-3,5 metri al massimo, ma anche minore se i pallini sono uniformi e non deformati. I pallini migliori si troveranno ovviamente nella parte anteriore e quelli deformati o più piccoli nella parte posteriore. Il centro più nutrito della sciame, che contiene circa il 75% dei pallini, si trova a circa un terzo (un metro circa) dai pallini anteriori.

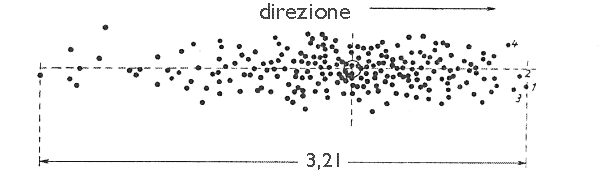
Sciame di pallini

Se si spara ad una lepre che passa di traverso a 35 metri, supposta una velocità finale di 226 ms per pallini di 3,5 mm, questi impiegheranno circa 0,144 secondi a colpire il bersaglio; siccome gli ultimi sono tre metri indietro ne impiegheranno 0,131 con una differenza di 0,013 secondi. Ammesso che la lepre abbia fretta e corra alla velocità di 15 ms, in quel tempuscolo potrà percorrere solo una ventina di centimetri e perciò non potra uscire dalla parte nutrita della rosata. Se però il cacciatore ha mirato bene, con il giusto vantaggio, in modo che i primi pallini colpiscano la testa, i pallini del centro dello sciame, a circa un metro dai primi, la colpiranno dopo che la lepre avrà percorso meno di 10 centimetri, vale a dire alla spalla. Se si fa lo stesso calcolo per un fagiano che viaggia a 25 ms di velocità, i dieci centimetri diventano circa 15.
Quale curiosità ricordo che certi cacciatori pasticcioni usavano mescolare pallini grossi a pallini piccoli convinti di avere così una cartuccia buona per tutti gli usi. È una emerita sciocchezza perché così facendo si ottengono, dopo una diecina di metri, due sciami perfettamente separati, ognuno dei quali contiene un numero di pallini del tutto insufficienti a uccidere il selvatico (a 35 metri i due sciami saranno ad una distanza, l'uno dall'altro, di circa 1,5 metri!).

Controllo della rosata
Esporrò qui il metodo ufficiale seguito in Germania per controllare la regolarità della rosata e che consente un'ottima valutazione di canne per caccia e cartucce. Per i fucili da tiro viene usato un diverso bersaglio.

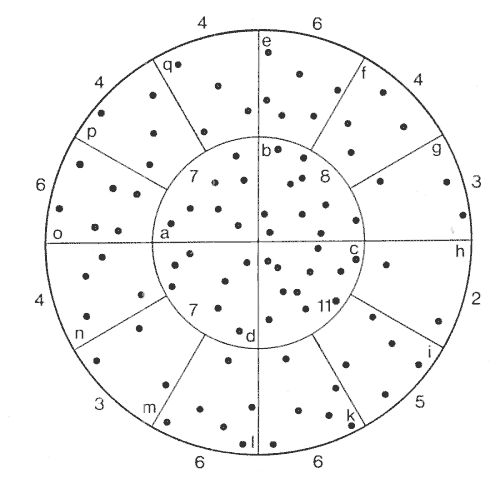
Bersaglio per prova della rosata

Il bersaglio di controllo è un cerchio di 75 cm di diametro con un cerchio interno di 37,5 cm. La corona circolare è divisa in dodici settori e il cerchio interno è diviso in quattro settori; ogni settore ha la superficie di 276, 125 cm². Questa misura è stata scelta in modo che due settori adiacenti (552 cm²) corrispondano alla superficie massima di una lepre, mentre una pernice corrisponde ad 1/3 di un settore (92 cm²) e un fagiano e un anatra a 2/3 (184 cm²). La prova viene effettuata sparando una serie di 5 cartucce eguali dalla distanza di 35 metri. Se una delle 5 rosata diverge dalle altre per più del 25% di impatti, occorre sparare altre cinque cartucce e la rosata anomala va scartata in quanto attribuibile ad anomalia della cartuccia.
Per ogni rosata si passa poi a valutare la copertura di ogni settore (due settori per la lepre) che sarà considerata sufficiente se, tenuto conto del diametro del pallino richiesto per l'animale in considerazione, si contano almeno:
- almeno 12 pallini da 2,5 mm in un settore e cioè almeno 4 pallini per la superficie di una pernice (1/3 di settore);
- almeno 6 pallini da 3 mm in un settore e cioè almeno 4 pallini per la superficie di un fagiano (2/3 di settore);
- almeno 6 pallini da 3,5 mm in due settori contigui, corrispondenti alla superficie di una lepre. In questo caso bisognerà sommare via via a+b, b+c, c+d, d+a, e+f,f+g,... fino a q+e. Nella figura è insufficiente solo il settore g+h e si hanno 89 pallini sul bersaglio con 15 settori coperti a sufficienza.
La rosata sarà tanto migliore quanto maggiore è il numero dei settori coperti e quanto maggiore è il numero di pallini complessivo. In presenza di un buon numero complessivo di pallini sul bersaglio, ma concentrati piuttosto sui settori centrali, non si deve concludere che l'arma spara male, ma solo che è più adatta per tiri lunghi; è perciò consigliabile di ripetere la prova a 40 metri di distanza.

Relazione tra selvatico e pallino
La balistica terminale della carica di pallini differisce fondamentalmente da quella del proiettile singolo. Questo deve trasferire la sua energia al corpo e quindi è costruito in modo da deformarsi e frantumarsi e da provocare distruzione meccanica dei tessuti, oltre a onde d'urto distruttive.
Diverso il comportamento della carica di pallini che è già frantumata e quindi scarica immediatamente e completamente tutta la sua energia su di una superficie molto maggiore. Si consideri che già alla bocca la carica di un calibro dodici ha una superficie di 2,5 cm², il che è otto volte quella di una palla calibro 8 mm. A cinque metri la superficie di impatto sarà 20-30 volte superiore ( 6-10 cm di diametro) con una energia di oltre 200 kgm (circa 2000 Joule) il che spiega l'effetto fulminante della carica a pallini a breve distanza, anche su animali di grossa taglia.
La carica di pallini conserva una energia sovrabbondante anche a distanze sui venti metri a cui, ad esempio, una lepre di 3 o 4 kg può essere colpita da un numero di pallini sufficienti a dare circa 30 kgm di energia, vale a dire quanto un buon calibro 38.
Il meccanismo dell'energia non è sufficiente a spiegare il motivo per cui il selvatico viene ucciso anche a distanza doppia sebbene colpito da un numero ridotto di pallini che talvolta penetrano di poco sotto la cute.
Il vero meccanismo è stato scoperto facendo esperimenti scientifici su animali: si è così visto che lo stesso animale che rimaneva fulminato da una scarica di pallini che appena bucavano la pelle, quasi non riportava danni se veniva colpito mentre era narcotizzato. Si è perciò concluso che la morte non deriva direttamente dalle ferite, di per sé lievi, ma dallo shock nervoso cagionato dal fatto che più pallini colpiscono contemporaneamente più terminazioni nervose sparse sul corpo. In medicina legale questo fenomeno è conosciuto come "morte per inibizione riflessa" che talvolta può verificarsi anche per una sollecitazione improvvisa di una singola piccola ridotta regione del corpo (gli atemi delle arti marziali o la morte improvvisa di chi si butta in acqua).
Per uccidere il selvatico è perciò necessario che venga colpito da un sufficiente numero di pallini che scatenino questo riflesso e paralizzino il cuore. Sotto questo aspetto può essere più letale una carica di pallini piccoli che una di pallini grossi, sempre che i pallini piccoli abbiano energia sufficiente a produrre ferite sotto cute.
Ovviamente un numero di pallini minore che penetrino in profondità entro il selvatico sono idonei ad ucciderlo, se colpiscono punti vitali o provocano emorragia, o ad immobilizzarlo se spezzano arti.
Nello scegliere il pallino si deve perciò cercare di ottenere entrambi i risultati con un pallino che assicuri sia una certa penetrazione sia un numero sufficiente di impatti, secondo il criterio sopra visto per la valutazione della rosata. Non si deve cercare di affidarsi solo alla penetrazione, ad esempio usando pallini molto grossi, perché diventa elevato il rischio che il selvatico passi tra i pallini indenne, oppure che venga ferito da uno solo e vada a morire altrove. Si deve poi tenere presente che l'effetto nervoso viene prodotto solo se i singoli pallini hanno una energia sufficiente a provocarlo. Ad esempio per una pernice si calcola che ogni pallino debba avere all'impatto una energia di almeno 0,11 - 0, 15 kgm. Questo non significa ovviamente che si possa sparare alla distanza di 100 metri se il calcolo teorico ci dice che un certo pallino possiede ancora l'energia richiesta a tale distanza! Rimane infatti ferma l'esigenza che il selvatico venga colpito da un numero sufficiente di pallini. Ad esempio i pallettoni da 8 mm potrebbero uccidere una volpe a 100 metri; però si devono usare a non più di 20-25 metri perché oltre tale distanza è un puro caso colpire la volpe con più di un pallino.
Il cacciatore che spara ad un selvatico con pallini più piccoli di quelli teoricamente più adatti, deve ricordarsi che deve ridurre la distanza di tiro; se spara con pallini più grossi corre il rischio di fracassare l'animale, se troppo vicino, o di mancarlo, se si trova oltre la distanza di copertura ottimale della rosata.
Secondo Journée la distanza massima a cui si può sparare ad un selvatico con buona sicurezza di ucciderlo, e non solo di ferirlo, è la seguente

In letteratura si trova talvolta cenno del fenomeno della "passata" che si verifica quando un selvatico in volo, trafitto da un singolo pallino, cade stecchito. Sono state escogitate varie teorie ma senza giungere a conclusioni definitive. È probabile che anche in questo caso insorga una specie di shock nervoso. Egualmente poco chiara è la ragione per cui, a seconda della carica delle cartuccia, talvolta l'uccello cada senza spargere una goccia di sangue, talvolta invece sanguini vistosamente dalla ferite.
Il "vantaggio"
Quando si spara ad un bersaglio in movimento non si deve mirare al centro di esso, ma un po' più in avanti, rispetto alla direzione del movimento, perché i pallini impiegano un certo tempo a raggiungere il bersaglio e in quel tempo il bersaglio si è spostato. Si consideri che sulla distanza di 35 metri i pallini viaggiano alla velocità media di 285 m/s e impiegano circa 0,12 secondi a percorrerla; se il selvatico vola a 20 ms, in tale tempo avrà percorso 2,4 m; se esso passa trasversalmente di fronte a noi si dovrà sparare a detta distanza davanti alla sua testa.
La formula per calcolare questo spazio è data da

(Velocità del selvatico) * (distanza) / (Velocità media pallini)

La velocità media si ottiene sommando velocità iniziale a velocità finale dei pallini e dividendo per due.
In teoria si dovrebbe tenere conto anche dei tempi di reazione del cacciatore e del sistema meccanico dell'arma, ma questi vengono corretti dallo stesso cacciatore che al momento dello sparo non blocca l'arma ma continua a muoverla, assecondando il movimento del bersaglio.
Se il bersaglio si muove in diagonale rispetto al cacciatore, il calcolo diviene molto più difficile; se il selvatico viaggia con un angolo di 70° rispetto alla linea trasversale, il che equivale a dire che la sua direzione di moto è di 20° rispetto alla linea di mira (si trascura qui la precisione teorica), il valore dello scostamento si otterrà moltiplicando il precedente valore per cos70° oppure per sen20°.
Nella pratica si ottiene lo stesso risultato utile calcolando il vantaggio non in metri, ma in "lunghezze dell'animale"; se un fagiano che vola trasversalmente ci appare lungo 60 cm il vantaggio da dare sarà dato da 240/60 = 4 fagiani; se esso si allontana in diagonale sarà sufficiente mirare "4 fagiani in avanti" secondo la lunghezza che il fagiano ci presenta per effetto della prospettiva.

La penetrazione del pallino
Circa la penetrazione di pallini in tessuti molli, sono stati fatti esperimenti su blocco di gelatina constatandosi che alla distanza di 35 metri e pallini da 2,5 mm la penetrazione è attorno ai 60 mm, se di 3 mm di diametro, la penetrazione è attorno ai 70 mm, se di 3,5 mm attorno agli 80 mm. Con pallini da 2,5 mm si è avuta, alle varie distanze, la seguente penetrazione

Munizioni a pallini per revolver Le cartucce per revolver sono vendute per la difesa da serpenti; esse sono caricate, nel cal. 38, con circa 135 pallini da 1,3 a 1,5 mm. Questa carica produce alla distanza di 15 metri una rosata di circa un metro di diametro. Essi, a tale distanza, non sono in grado di superare un abbigliamento invernale.
Al fine di usare queste cartucce anche per difesa personale non letale, sono state fatte prove con pallini di dimensioni maggiori.
Con pallini da 2,5 mm la rosata è ancora nutrita, ma anch'essi a 15 metri di distanza riescono appena a penetrare oltre un cappotto, senza ferire la cute. Con pallini da 3,5 mm si producono ferite. I pallini da 4,5 mm superano agevolmente gli abiti e penetrano per 3 cm in un blocco di plastilina; però in una cartuccia ve ne stanno solo una ventina. Si è quindi pensato di caricare queste cartucce con una miscela di pallini di varie dimensioni, in modo da avere una rosata nutrita e aumentare l'effetto di shock. La miscela più congrua è risultata quella con il 50% di pallini da 2,5 mm, il 25% da 3,5 mm e il 25% da 4,25 mm., con un totale di circa 50 pallini. Usando polveri e cariche vivaci (ad es. 4,5 grani di Kemira N 310) si ottengono velocità di poco inferiori ai 300 ms in canne da 3 pollici.
Con queste cartucce si è riscontrato che una sagoma umana veniva colpita da circa 40-45 pallini a 5 metri, da 25-35 pallini a 10 metri, da 20-25 pallini a 15 metri. Oltre questa distanza, la rosata risulta molto sguarnita al centro.
A distanza ravvicinata tutti i pallini perforano 15 mm di legno; a 5 metri passano quelli da 3,5 e 4,25 mm, a 10 metri solo alcuni dei pallini da 3,5 riescono a passare, a 15 metri solo quelli da 4,25 passano (al 90%)
Invece la penetrazione nella plastilina, dopo aver superato 5 mm. di strati di tessuto, è stata la seguente

La penetrazione dei pallini da 4,25mm nella plastilina non protetta da tessuto è stata di 30 mm. La probabilità di colpire agli occhi, sparando a 15 metri, è risultata dello 1%

Bibliografia
Lampel W, Jagdballistik, Melsungen 1971
Lampel - Marhold, Waffen Lexikon, München 1994
Haglund B. - Claesson E. (Husqvarna) , Mina Jaktvapen, Stockholm 1957
Burrard, The modern Shotgun, 3 vol. , London 1952
Journée, Tire des Fusils de Chasse, Paris 1947
v. Wissman, Der Schrotschuss, Hamburg 1968

email - Edoardo Mori	top

Sitemap: in Italiano | auf Deutsch | in English |

http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003