
 |
| back |

Il comportamento della rosata è stata oggetto di ampi
studi, anche da parte di Autori italiani e si rimanda alla apposita pagina, anche per i problemi di balistica terminale; qui ci limiteremo all'esame
della possibilità di calcolo numerico delle traiettoria
di singoli pallini componenti la rosata.
I pallini, quando escono dalla bocca dell'arma, formano un blocco
ancora alquanto compatto, salvo pochi pallini deviati in modo
anomalo per urti contro il vivo di volata. Già a pochi
metri dall'arma però, l'aria si fa strada fra i singoli
pallini i quali iniziano a risentire l'influsso della sua resistenza
in modo diverso, a seconda del peso e delle deformazioni subite
per il contatto con l'anima della canna, o per compressioni nella
cartuccia o per urti reciproci, ecc. I pallini vengono così
a formare uno sciame allungato con la maggior concentrazione verso
la sua parte anteriore (il centro di gravità della rosata
si colloca a circa 2/3 della sua lunghezza).
Per calcoli di estrema precisione, quali non si richiedono nella
pratica venatoria, deve tenersi presente il fatto che la resistenza
dell'aria sui singoli pallini che si trovano ancora molto ravvicinati
l'uno all'altro, è minore di quella che il pallino subirebbe
se fosse isolato. Di conseguenza i pallini sparati da una canna
strozzata presentano una diminuzione di velocità minore
rispetto ai pallini sparati da una canna cilindrica, ed ancora
minore rispetto ad un pallino sparato singolarmente.
Per il calcolo della ritardazione subita dai pallini si può
far ricorso alle tavole dello Ingalls o del Lovry (ed ovviamente
al software basato su di esse), ma non è facile impostare
il giusto coefficiente balistico che esse calcolano per proiettili
non sferici. Ad esempio, impiegando le tavole del Lovry, si ottengono
risultati esatti se, per una velocità iniziale di 360 ms,
si adotta il coefficiente i = 2,2 per pallini di 3-4 mm di diametro,
mentre per pallini di 2 mm. il coeff. è pari a 2,4. Per
la palla sferica di 18,5 mm. il coeff. diventa pari a 1,65.
Formula approssimativa
Per un calcolo approssimativo della perdita di velocità
di un proiettile su di una determinata tratta si può ricorrere
alla seguente formula, precisa per pallini di 4 mm, ma accettabile
per pallini da 2 a 6 millimetri di diametro nell'ambito delle distanze
venatorie (25-60 metri).
La formula è
![]()
in cui V è la velocità finale, D la tratta in metri e d il diametro del pallino in mm.
Calcolo preciso
Per una maggior precisione si può far ricorso alle tavole
di ritardazione compilate dal Journée proprio per palle
sferiche e di cui riportiamo più sotto un estratto.
L'uso delle tavole è il seguente.
Prima di tutto occorre calcolare il coefficiente balistico della
palla
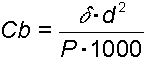
in cui d è il diametro in mm e P il peso in grammi e
indica la densità dell'aria (standard = 1,22).
Ricordo che il peso di una palla, per una densità standard
del piombo di 11,1 gr per centimetro cubo, è data da
A titolo di esempio si veda come il Cb di un pallino di 3 mm sarà
pari a 0,07 e quello di una palla sferica cal. 12 (18,5 mm) di
0,0115.
Sia ora da calcolare la velocità residua a 100 metri della
palla sferica cal .12 sparata con la velocità iniziale
di 360 ms.
Dalla tavola si legge che il valore R relativo a V=360 è
1,6208; a questo valore si aggiunge ora il valore del coefficiente
balistico moltiplicato per la distanza considerata e quindi
Cb · 100 = 0,01128 · 100 = 1,128;
R= 1,128 + 1,6208 = 2,7488 Gittata massima dei pallini
in corrispondenza del quale leggiamo la velocità ricercata,
pari a poco meno di 260 ms. (il valore esatto può ricavarsi
per interpolazione).
Tempi di volo
La seconda colonna della tavola (i cui valori vanno divisi per
100) consente di calcolare il tempo di volo. Proseguendo nell'esempio
appena fatto, in corrispondenza di V=260, si legge il valore T
= 0,007010 e in corrispondenza di V = 360, T = 0,003290
Il tempo di volo sarà dato dalla differenza di questi due
valori divisa per il coefficiente balistico e quindi 0,00372 :
0,01128 = 0,329 secondi.
Una volta calcolati i tempi di volo e le velocità residue
alle varie distanze, gli altri elementi della traiettoria possono
essere calcolati con i sistemi noti per proiettili di armi a canna
rigata.
La gittata massima dei pallini si ottiene con angoli di proiezione
che vanno dai 14° per i pallini da 1 mm a 25° per la
palla cal. 12. In modo molto empirico, la gittata può
assumersi essere pari a tanti metri quanti dà il prodotto
di 80 per i diametro del pallino (quindi il pallino di 3 mm arriverà
a 240 metri).
Un risultato più soddisfacente (valido dal pallino da 1
mm. fino alla palla cal. 12) è fornito dalla formula
Dispersione dei pallini
Il diametro della rosata non aumenta in modo lineare con l'aumentare
della distanza; vale a dire che se a 10 metri la rosata ha un
diametro di 15 cm, alla distanza di 20 metri essa non sarà
di 30 cm, ma un poco più ampia.
È impossibile fornire una regola matematica che consenta
di calcolare con precisione la dispersione dei pallini, anche
perché ogni strozzatura ha, in definitiva, un suo particolare
comportamento.
A titolo puramente orientativo si può utilizzare la formula
la quale ci dice che si assume eguale ad 1 il raggio del circolo
che a 5 metri dall'arma contiene il 50% dei pallini, il raggio
alla distanza x sarà pari a y volte; in
altre parole se a 5 metri il raggio del circolo contenente il
50% dei pallini è di 3, 5 cm, a 60 metri il raggio di tale
circolo sarà di 22 volte più grande e quindi di
22 . 3,5 = 77 cm.
Si tenga presente che questo è un valore intermedio per
pallini di circa 2, 5 mm. e che la rosata per pallini di minor
diametro è un po' più ampia e quella per pallini
più grossi, un poco più ristretta.
TAVOLA DI JOURNÉE
Velocità R T·100 -------------------------------------- 30 16,612 19,94 35 15,654 17,23 40 14,696 14,50 45 13,952 12,86 50 13,208 11,21 55 12,600 10,11 60 11,993 9,007 65 11,479 8,217 70 10,965 7,429 75 10,553 6,836 80 10,142 6,244 85 9,7486 5,782 90 9,3556 5,321 100 8,6541 4,583 105 8,3376 4,382 110 8,0211 3,980 115 7,7326 3,730 120 7,4441 3,479 125 7,1794 3,267 130 6,9146 3,056 135 6,6706 2,875 140 6,4266 2,694 145 6,2006 2,538 150 5,9746 2,283 155 5,7651 2,253 160 5,5556 2,124 165 5,3601 2,006 170 5,1646 1,887 175 4,9913 1,783 180 4,8179 1,679 185 4,6479 1,587 190 4,4779 1,495 195 4,3192 1,414 200 4,1604 1,332 205 4,0122 1,260 210 3,8639 1,118 215 3,7272 1,124 220 3,5904 1,060 225 3,4667 1,006 230 3,3429 0,9507 235 3,2294 0,9025 240 3,1159 0,8542 245 3,0152 0,8130 250 2,9144 0,7719 255 2,8241 0,7365 260 2,7337 0,7010 265 2,6522 0,6696 270 2,5707 0,6389 275 2,4970 0,6113 280 2,4233 0,5845 285 2,3566 0,5611 290 2,2899 0,5377 295 2,2290 0,5170 300 2,1682 0,4964 305 2,1127 0,4782 310 2,0571 0,4600 315 2,0064 0,4439 320 1,9556 0,4278 325 1,9091 0,4135 330 1,8626 0,3992 335 1,6197 0,3864 340 1,7767 0,3735 345 1,7365 0,3619 350 1,6963 0,3502 355 1,6585 0,3396 360 1,6208 0,3290 365 1,5851 0,3197 370 1,5594 0,3094 375 1,5154 0,3004 380 1,4814 0,2913 385 1,4489 0,2829 390 1,4164 0,2744 395 1,3851 0,2665 400 1,3538 0,2586 405 1,3237 0,2512 410 1,2936 0,2437 415 1,2645 0,2367 420 1,2354 0,2297 425 1,2073 0,2231 430 1,1791 0,2165 435 1,1518 0,2102 440 1,1244 0,2039 445 1,0979 0,1980 450 1,0713 0,1920 455 1,0454 0,1863 460 1,0195 0,1806 465 0,99422 0,1752 470 0,96897 0,1698 475 0,94429 0,1646 480 0,91960 0,1594 485 0,89545 0,1544 490 0,87130 0,1494 495 0,84765 0,1446 500 0,82400 0,1399 505 0,80079 0,1353 510 0,77758 0,1307 515 0,75478 0,1262 520 0,73196 0,1218 525 0,70958 0,1177 530 0,68718 0,1133 535 0,66513 0,1092 540 0,64308 0,1050 545 0,62147 0,1011 550 0,59986 0,09707 555 0,57844 0,09321 560 0,55701 0,08935 565 0,53586 0,08561 570 0,51470 0,08187 575 0,49381 0,07805 580 0,47292 0,07424 585 0,45228 0,07071 590 0,43164 0,06718 595 0,41119 0,06375 600 0,39074 0,06032 605 0,37048 0,05697 610 0,35022 0,05362 615 0,33015 0,05036 620 0,31007 0,04709 625 0,29022 0,04391 630 0,27037 0,04072 635 0,25036 0,03762 640 0,23089 0,03451 645 0,21131 0,03147 650 0,19173 0,02844 655 0,17228 0,02547 660 0,15283 0,02250 665 0,13353 0,01960 670 0,11422 0,01669 675 0,09506 0,01385 680 0,07589 0,01101 685 0,05683 0,00823 690 0,03777 0,00545 700 0,00000 0,00000
Si veda ancha la pagina sulla rosata
| Sitemap: in Italiano | auf Deutsch | in English | |
| http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003 |