Dr. Felice Nunziata - Il tiro verticale e la ricaduta del proietitle - Un po' di balistica teorica.

Se provassimo a descrivere in termini spazio-temporali tutti i corpi che precipitano nel vuoto, ossia trascurando in prima approssimazione gli effetti di attrito dell`aria, noteremmo, contrariamente al senso comune veicolato dalle esperienze quotidiane, che essi posseggono la stessa accelerazione, indipendentemente dalla loro massa.
A conti fatti noteremmo che l`accelerazione varrebbe circa 9,81 m/s2: questa valutazione appare ovvia alla luce della legge che esprime la forza di Gravitazione Universale:

dove:
M è la massa della Terra;
G è la costante gravitazionale;
mg è la massa del corpo soggetto alla forza gravitazionale;
r è la distanza del corpo dal centro della terra
In prossimità della superficie terrestre la quantità

   
vale proprio 9,81 m/s2.
Nel caso in cui lanciamo un oggetto sulla nostra verticale, l`equazione oraria, nell`approssimazione dell`assenza dell`aria, è rappresentata da quella che descrive il moto uniformemente accelerato

La descrizione si complica (e di molto) se invece introduciamo nei nostri ragionamenti la presenza dell`aria.
Infatti, l`aria essendo un gas appartiene alla famiglia dei fluidi ossia è un particolare stato della materia che gode, tra l`altro, della proprietà di deformarsi illimitatamente se sottoposto a uno sforzo di taglio.
Noi ci limiteremo alla descrizione del moto relativo di un corpo all`interno del fluido aria, nel caso in cui il corpo descriva una traiettoria verticale.
In prima approssimazione descriviamo il moto di un corpo che si muove all`interno del fluido aria e che risente, in assenza di altre forze, della forza risultante dovuta agli attriti indotti dal fluido stesso.
Questa forza risultante, ricavata da una serie di valutazioni empiche, risulta del tipo
FA (v) = - kv2
per cui il Secondo Principio della Dinamica si riscrive come

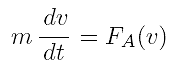
Separando le variabili otteniamo

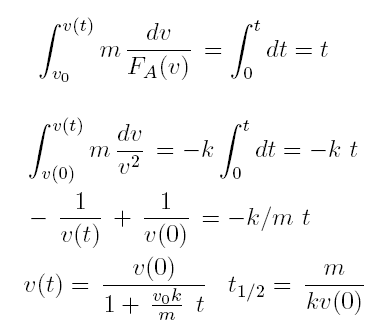
Nel caso più realistico, ma più complesso, della presenza della forza di gravita` ricercando la condizione per cui  

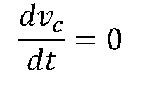
otteniamo una condizione che ci permette di risolvere agevolmente i problemi di natura analitica.

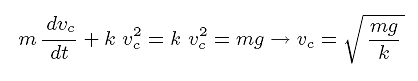
Il caso della traiettoria verticale, a causa dell`intrinseca geometria collineare delle forze in campo ossia gravità e attrito dell`aria, garantisce risultati analitici soddifacentemente rappresentativi della realtà.
Limitiamoci al caso di una sfera di raggio R e massa m che subisce a causa dell`attrito dell`aria (la cui densità possiamo porla pari a ρ  = 1,29 kg/m3) una forza (opposta al moto della stessa) del tipo

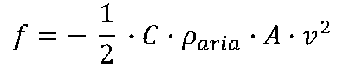
dove per una sfera C = 0,5.
Come abbiamo già affermato la soluzione dell`equazione differenziale si ottiene imponendo che la  f  sia uguale alla forza peso; quindi la velocità vc sarà

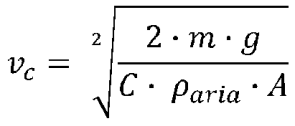
  da cui il tempo caratteristico  

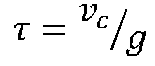
Schematizziamo il lancio verso l`alto di un grave di forma sferica dotato di vo mediante un disegno che rappresenta le fasi ascendente, apicale, discendente e quella dell`impatto al suolo.

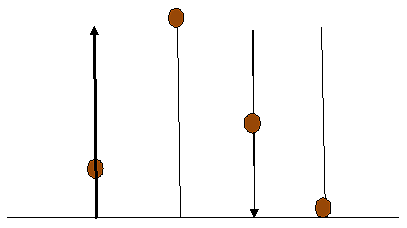
 Nel tratto ascendente , con velocita`iniziale vo abbiamo:

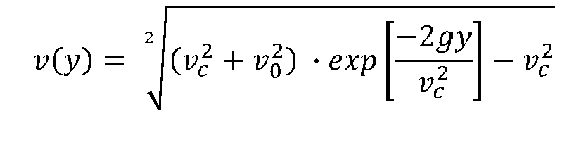
Nella parte apicale della traiettoria abbiamo:

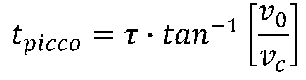
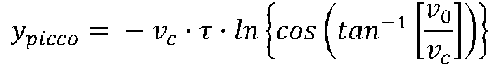
Nel tratto discendente abbiamo:

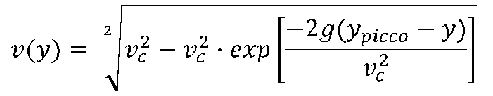
Infine all`impatto con il suolo:

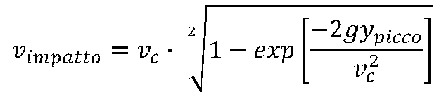
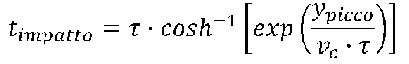
ALLEGATO: file con le fomule già impostate per i calcoli
Si veda questa pagina per una esposizione più divulgativa

xxx