
 |
| back |

Il tiro verticale rappresenta un caso particolare di traiettoria. La velocità decresce fino ad
essere nulla al vertice della traiettoria (che è rettilinea) e poi il proiettile ricade per il
solo effetto della forza di gravità.
Nel vuoto l'altezza massima raggiunta è data dalla formula
![]()
Nell'aria l'altezza massima raggiunta può essere calcolata con la formula empirica
in cui P è il peso in grammi, V la velocità in ms, Cal il calibro in mm e in cui la
costante varia da 220 per proiettili appuntiti a 185 per proiettili a punta tonda.
In via molto approssimativa può ritenersi che l'altezza massima sia pari al 70% della gittata
massima.
Esempio: Sia il proiettile 8x57 JS con Vo =870 ms e P=10 gr
Usando il coefficiente 220 si avrà H= 2565 del tutto corrispondente a quella sperimentale.
Per un proiettile 9 para e V = 330 ms, il valore sperimentale è di 1143 metri; per un 7,65 e
V =. 300 ms, è 932 metri.
Il tempo impiegato dal proiettile a raggiungere la sua altezza massima nell'aria può essere
calcolato, con buona approssimazione, mediante la formula
![]()
Ricordiamo che nel vuoto avremmo avuto
![]()
Nell'esempio visto per il calibro 8x57 avremmo quindi t = 18,7 secondi.
La caduta libera del proiettile nell'aria richiede un esame più approfondito. Esso cadendo
acquista un modo accelerato, frenato dalla crescente resistenza dell'aria. Ad un certo punto si
verificherà però che la forza ritardatrice della resistenza dell'aria eguaglia la forza
di gravità; da quel momento le due forze si equilibrano e il moto diventa uniforme, la
velocità diviene costante. È per questo motivo che un chicco di grandine di media
grandezza non giunge a terra con una velocità pericolosa, ma a circa 50 ms. Un paracadute, che
ha un'ampia superficie, rallenta la velocità di caduta del paracadutista fino a circa 6 ms; ma
anche il paracadutista che scende in caduta libera raggiunge, dopo circa 300-400 metri, la
velocità massima (cosiddetta velocità limite), che è di circa 50 ms.
Ciò avviene anche per i proiettili e le bombe d'aereo.
Posto che la ritardazione è data da
Ritardazione = (Resistenza x Gravità) / Peso
e che l'accelerazione di gravità è pari a 9,81 m/sec², la situazione di equilibrio sarà data quando
![]()
e cioè quando R = P
La resistenza R è espressa dalla formula R = Cb·f(v) e perciò si tratterà
semplicemente di trovare per quali valori di v si ha Cb·f(v) = P in relazione a un dato proiettile.
Facciamo un esempio pratico.
Sai il proiettile 8x57 e sia P= 0,0128 kg e il coeff. di forma i = 0,65.
Il coefficiente balistico sarà dato da
![]()
da cui 0,326·f(v) = 0,0128 = R
e quindi f(v) = 0,0128/0,326 = 0,039
Dalle tavole di Sängewald si legge che f(v) 0,039 corrisponde a 180 ms, che è la
velocità limite del proiettile in esame.
Per un proiettile 9 para si otterrebbe un valore di 96 ms
Ovviamente la velocità limite non potrà mai essere superiore alla
velocità che il proiettile avrebbe acquistato nel vuoto secondo la
formula
Il calcolo è valido per proiettili di piccolo calibro che non raggiungono altezze rilevanti,
così da poter considerare costante la densità dell'atmosfera attraversata.
Esso è valido inoltre solo nel caso che il proiettile ricada con la punta in avanti.
Se si dispone del coefficiente auerodimamico la formula diventa
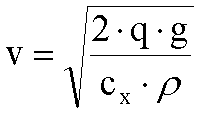
in cui q = densità sezionale, kg/mq;
? = densità dell'aria
Se invece ricade senza capovolgersi, con il fondello verso il basso, aumenta notevolmente il fattore
di forma. Un proiettile cal. 9 para, ad esempio, avrebbe un fattore di forma di 2,30 invece che di
1,2 e la sua velocità limite sarebbe di circa 70 ms.
Le esperienze compiute hanno dimostrato che il proiettile ricadente, se non riesca a capovolgersi per
effetto di una certa angolazione del tiro rispetto alla perpendicolare o per effetto del vento, ricade
con la base verso il suolo e roteando vorticosamente con un tipico ronzio, così che viene ad
avere un fattore di forma pari a 7,5 e una velocità limite non superiore a 40 ms.
In base ai dati teorici e sperimentali si può concludere che il proiettile sparato verticalmente
e non capovoltosi (il che però richiede una traiettoria quasi perfettamente verticale) ricade
con una velocità bassa, non idonea a ledere la persona. Il proiettile che al vertice della
traiettoria segue la normale curvatura di questa e ricade con la punta in avanti acquista invece
una velocità superiore a 100 ms e può essere pericoloso; un proiettile cal 9 para, ad
esempio, come detto nell'apposito capitolo di balistica terminale, alla velocità di 100 ms
può perforare la cute e produrre ferite superficiali. Un proiettile appuntito per fucile
militare può perforare la cute e almeno 40 cm di tessuto molle o un cm di osso!
Il proiettile di fucile sparato verticalmente, se non spostato dal vento, ricade entro un raggio di
10 metri dal tiratore; ma il vento può spostarlo anche di 200 metri.
È quindi molto pericoloso sparare in aria con proiettili appuntiti.
Vediamo ora il tempo totale di volo di un proiettile sparato verticalmente.
Abbiamo già visto che il tempo di salita può essere calcolato con la formula
![]()
Per calcolare poi il tempo di caduta con una certa approssimazione, supponiamo che il primo tratto del percorso venga compiuto nel vuoto, stante la limitata resistenza iniziale dell'aria e che sia quindi (Vl = velocità limite):
e che quindi il tempo impiegato a percorre il tratto sia dato da
![]()
Il resto della traiettoria (h - h1) verrà invece percorso a velocità costante e quindi nel tempo
![]()
Esempio: Sia un proiettile cal. 9 para in cui V = 330 ms, P = 8,5 gr, Vl= 70 ms (cade capovolto), da cui y/max = 1143 m e tempo di salita 12,5 secondi.
E quindi, con le formule viste
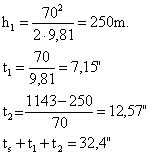
Esperimenti compiuti con il proiettile 8x57 appuntito e sparato capovolto, in modo da avere la sicurezza che ricadesse con la punta in avanti, hanno stabilito un tempo totale di 31". Lo stesso proiettile, sparato normalmente e in modo perfettamente verticale, impiegò invece ben 74" a ricadere; questo risultato si ottiene supponendo che nella fase di caduta esso avesse un coefficiente di forma pari a 7,5
Bombe di aereo
La caduta di una bomba da un 'aereo è soggetta alle stesse leggi che regolano la traiettoria di
un proiettile.
Nel vuoto la bomba continua a viaggiare con la stessa velocità dell'aereo e si trova quindi
sempre perpendicolarmente sotto di esso.
Le formule per la caduta nel vuoto sono facilmente calcolabili.
Se l'aereo viaggia alla velocità Va e con l'angolo theta rispetto all'orizzonte le equazioni
del movimento saranno
![]()
e
da cui l'equazione della traiettoria
Questa formula si distingue da quella vista per i proiettile per il fatto che il movimento dovuto
alla forza di gravità si aggiunge sempre al restante movimento.
Da questa formula si ricava la distanza di lancio in base all'altezza y
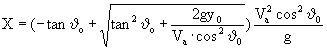
Quindi la bomba cadrà tanto più lontano quanto più grandi sono la velocità
dell'aereo e la sua altezza e quanto più piccolo è l'angolo di picchiata.
Il tempo di caduta si ricava dalla formula
Se l'aereo procede in orizzontale e quindi theta = 0, si avrà
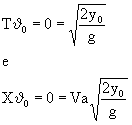
Nell'atmosfera il movimento orizzontale della bomba verrà frenato dalla resistenza dell'aria e la bomba resterà indietro rispetto all'aereo. La distanza di lancio X sarà anch'essa ridotta rispetto a quella Xo nel vuoto. La bomba poi cadrà più lentamente per effetto della resistenza dell'aria e quindi impiegherà maggior tempo a raggiungere il suolo con la conseguenza che l'aereo, il quale viaggia a velocità costante, verrà a trovarsi ancora
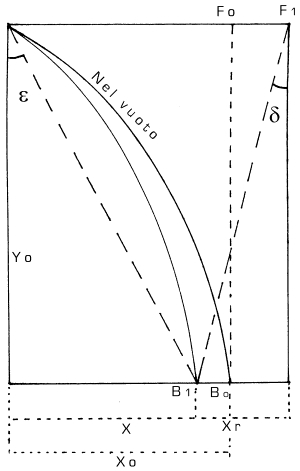
più avanti rispetto alla perpendicolare al punto di caduta (cioè nel punto F1 invece
che nel punto Fo) e anche l'angolo di impatto sarà maggiore. La velocità finale di caduta
dipenderà dalla forma della bomba, oltre che dall'altezza di caduta.
Si tenga presente che i valori della velocità di caduta differiscono in misura alquanto modesta
da quelli nel vuoto. Ecco alcuni dati sperimentali in base all'altezza di lancio.
| Altitudine m. | 250 Kg cal. 15,5 | 500 Kg cal.21 | Nel vuoto |
3000 |
232 |
234 |
243 |
4000 |
264 |
267 |
280 |
5000 |
288 |
292 |
314 |
6000 |
307 |
314 |
344 |
7000 |
324 |
335 |
371 |
In base poi alla forma e al peso si avrà per ogni bomba una velocità limite di caduta insuperabile. Ad esempio per una bomba da 45 kg la velocità limite è di 274 ms mentre per una bomba da 900 kg si arriva fino a 518 ms
Il tratto Xr di cui la bomba rimane indietro rispetto all'aereo dicesi distanza di arretramento e
l'angolo sotto cui il punto d'impatto B1 viene visto dall'aereo dicesi angolo di arretramento (non
sono sicuro che sia il termine usato in aviazione!) che
in pratica può essere ritenuto non variare con il variare dell'altitudine.
La bomba dovrà essere lanciata quando l'aereo si trova alla distanza orizzontale X dal bersaglio;
in quel momento lo vedrà sotto l'angolo epsilon (angolo di ingaggio del bersaglio).
Per tale tiro valgono le formule
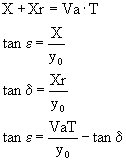
in cui T è naturalmente il tempo di caduta nell'atmosfera. L'angolo epsilon viene quindi calcolato in base alla velocità
dell'aereo, all'altitudine, al tempo di caduta e all'angolo di arretramento e ai fattori di disturbo
(caratteristiche dell'atmosfera, vento, ecc.).
Vediamo un esempio di calcolo.
Sia H= 4000 metri, T= 31,7" (nel vuoto 28,6") e la velocità dell'aereo Va= 50 ms
I dati sperimentali della bomba ci dicono che in tali condizioni lo spazio di arretramento Xr è
pari a 212 metri e quindi l'angolo di arretramento sarà dato da
da cui si calcola la distanza di lancio
X= Va ·T - Xr = 50 · 31,7 - 212 = 1373 m.
Vale a dire che la bomba dovrà essere lanciata quando l'aereo è a 1373 metri dal bersaglio,
in orizzontale.
L'angolo di ingaggio sarà dato da
| Sitemap: in Italiano | auf Deutsch | in English | |
| http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003 |