search

	Home > Balistica > Sottomenu > Documento	back

BALISTICA INTERNA

Volata di una canna con rigatura ed i "pieni" e "vuoti".

La balistica interna studia i fenomeni che accadono dal momento della percussione dell'innesco della cartuccia fino al momento in cui il proiettile esce dalla bocca dell'arma, divenendo oggetto di studio della balistica esterna.
A seguito della violenta percussione del percussore sulla capsula dell'innesco, la composizione innescante viene schiacciata contro l'incudinetta della capsula (nel caso della percussione anulare l'innesco viene schiacciato contro il metallo dell'orlo del fondello); la composizione esplode (volgarmente si dice che detona, a ricordo degli inneschi ottocenteschi al fulminato di mercurio; ora però la miscela usata non è più detonante) producendo un intenso dardo di fiamma che, attraverso i fori dell'innesco, raggiunge la carica di polvere, dando inizio alla sua deflagrazione.
Questa sarà più o meno veloce in relazione alla forza dell'innesco, al tipo, conformazione e quantità della polvere, alla densità di caricamento (rapporto tra volume della polvere e spazio nella cartuccia), alla compressione esercitata sulla polvere, alla forza con cui il proiettile è trattenuto dal bossolo, ecc.. La polvere deve poter bruciare completamente prima che il proiettile esca dalla canna, sia perché così tutta l'energia viene sfruttata, sia per evitare che i residui si infiammino fuori della bocca dell'arma (vampa di bocca).
La polvere brucia sempre perpendicolarmente alla sua attuale superficie e la quantità di gas prodotti dipende in ogni istante dalla pressione sviluppatasi e dalla forma geometrica dei granelli di polvere. Se la superficie del granello diminuisce durante la combustione (granelli tondi o a lamelle), si ha una polvere degressiva (offensiva), se aumenta (grani o tubetti con più fori) si ha una polvere progressiva; se rimane costante (tubetto con un foro) si ha una polvere neutrale. La velocità di deflagrazione può venire influenzata da trattamenti della superficie del grano.
Le polveri offensive sono più indicate per armi a canna corta in cui non ha senso una pressione che si esplica dopo che il proiettile ha abbandonato l'arma; le polveri progressive sono preferite nelle armi a canna lunga e in tutti quei casi in cui si preferisce non sottoporre ad eccessive sollecitazioni le pareti dell'arma.
La deflagrazione della polvere sviluppa una grande quantità di gas (circa un litro per ogni grammo di polvere) che si dilatano per effetto del calore (oltre 2000 gradi); un litro di gas, racchiuso in uno spazio minimo e sottoposto a tale temperatura produce un aumento di pressione che in un fucile a palla giunge a superare i 3000 kg/cm² (circa 500 atmosfere in un fucile a canna liscia). La pressione così sviluppatasi si esercita in tutte le direzioni: contro le pareti del bossolo che viene pressato contro la parete della camera di cartuccia (così assicurando che non sfuggano gas all'indietro), contro il fondello che viene premuto contro l'otturatore, contro il fondo del proiettile che viene spinto in avanti; essa continua a crescere fino al momento in cui il proiettile si svincola dal bossolo e inizia il suo percorso. aumenta quindi lo spazio a disposizione per i gas, ma fino a che la produzione di gas è maggiore dello spazio a disposizione, continua ad aumentare la pressione, il che aumenta la produzione di gas. Raggiunto l'equilibrio tra i due valori, la pressione inizia a calare. La combustione deve essere regolata in modo da non superare certi valori di pressione massima e di pressione alla bocca ed in modo che la combustione si concluda all'interno della canna. Il picco di pressione massima si verifica molto presto, in genere da alcuni millimetri a pochi centimetri di percorso del proiettile e la pressione alla bocca deve essere cinque o sei volte minore.
Durante il percorso nella canna il proiettile viene costantemente accelerato nel suo moto così che esce dalla bocca con il massimo della velocità. La pressione invece si riduce a poche centinaia di atmosfere. In genere in un'arma leggera l'aumento della lunghezza della canna non comporta alcun aumento della velocità del proiettile oltre i 60-70 cm. di lunghezza. Nelle armi a canna liscia a pallini, accurati esperimenti hanno dimostrato che, a parità di strozzatura, oltre i 60 cm di lunghezza si ha un aumento di velocità pari a circa 1 m/s per ogni centimetro in più e quindi, nella pratica, un aumento trascurabile.
Un parametro importante nei calcoli di balistica interna è data dal "rapporto di espansione" (inglese: expansion rate) che dà il rapporto tra pressione massima, pressione alla bocca, volume interno della canna e volume interno del bossolo:

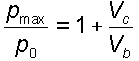
Altro importante parametro è dato dal rapporto tra pressione media e pressione massima.
Il valore della pressione media è dato dalla formula

in cui
m = peso del proiettile in g (dovrei dire massa, ma peso è più chiaro!)
mc = peso della polvere in g
Vo = velocità alla bocca in m/s
S = sezione della canna in mm quadrati
L = spazio libero percorso dal proiettile
Il valore della pressione massima deve essere misurato sperimentalmente oppure ricavato dalle tabelle dele munizioni o di ricarica delle varie polveri.

Calcoli di balistica interna

Il balistico tedesco Heydenreich, sulla base di esperimenti compiuti all'inizio del secolo, ha elaborato una serie di formule empiriche che consentono di eseguire i principali calcoli di balistica interna con accettabile approssimazione.
Sia
Pm = pressione media
Pmax = Pressione massima
Xpmax = Spazio percorso dal proiettile fino al raggiungimento della pressione massima
Vpmax = Velocità del proiettile al raggiungimento della pressione massima
Tpmax = Tempo impiegato a raggiungere la pressione massima
Po = Pressione alla bocca
Xo = Percorso del proiettile fino alla bocca
Vo = Velocità del proiettile alla bocca
To = Tempo impiegato dal proiettile per raggiungere la bocca
Px = Pressione dopo che il proiettile ha percorso lo spazio x
Vx = Velocità dopo che il proiettile ha percorso lo spazio x
Tx = Tempo impiegato a percorrere lo spazio x
I valori ricercati potranno essere calcolati agevolmente mediante l'uso della prima tabella di valori, sulla base della conoscenza di

con le seguenti formule:

Una seconda tabella consente invece di calcolare pressione, velocità e tempi in relazione allo spazio percorso, conoscendo il valore

del rapporto tra spazio percorso e Xpmax.
Le formule da applicare sono:
Px = Pmax · G
Vx = Vpmax · H
Tx = Tp · J
Quindi, se sono noti la pressione massima e la velocità alla bocca di una cartuccia, è possibile calcolare i valori lungo tutto il percorso del proiettile entro la canna.
Vediamo un esempio pratico di calcolo (da Beat P. Kneubuehl, Geschosse, 1994)
Sia un proiettile cal. 38 del peso di g. 10,2. Il peso della polvere sia 0,26 g., lo spazio libero percorso dal proiettile 123 mm, (alla lunghezza della canna va aggiunta la lunghezza del proiettile) la velocità alla bocca 265 m/s, la pressione massima 1600 bar, la sezione della canna 62,77 mm quadrati. Si avrà

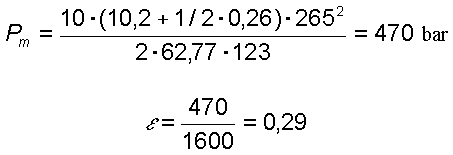
E quindi:
Xpmax = 123·0,0383 = 4,7 mm
Tpmax = [(2·)/265] · 0,165 = 0,15 ms
Vpmax = 265 ·0,331 = 87,7 m/s
Po = 470 · 0, 237 = 111 bar
To = [(2·123)/265]·0,754= 70 ms
Il valore di

sarà dato da 123/ 4,7 = 26,17

Le formule non tengono conto della perdita di pressione tra tamburo e canna nei revolver.

A titolo di esempio riporto i seguenti dati sperimentali circa le pressioni e la velocità dei gas alla bocca:

Velocità dei gas alla bocca
I gas di sparo escono dalla bocca con grande velocità che, per le pistole, supera quella del proiettile; essi quindi, per un breve tratto, oltrepassano il proiettile.
La velocità dei gas può essere calcolata con la formula di Laval

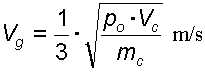
in cui Vc è il volume della canna e del bossolo in mm cubi ed mc è la massa dellapolvere in g . In essa, per semplificazione, si presume che al mometo dell'uscita del proiettile la pressione sia eguale in tutta la canna+ bossolo.

La velocità del proiettile a seconda della lunghezza della canna - Calcolo semplificato.
La velocità del proiettile, oltre che dal tipo di cartuccia, dipende da vari fattori quali la maggiore o minore marcata forzatura fra le righe della canna, la perdita di energia meccanica conseguente all'attrito all'interno dell'anima, dalle condizioni atmosferiche che influenzano la combustione della carica di lancio, per tacere poi dello stato di conservazione della cartuccia.
In genere i fabbricanti indicano la velocità del proiettile delle loro cartucce; i dati sono in genere riferiti a canne di prova di 60 cm di lunghezza, con caratteristiche ottimali, e sono valori medi che possono divergere anche del 5% rispetto alla velocità effettiva. Quando non sia possibile misurare direttamente la velocità del proiettile, ci si dovrà affidare a calcoli teorici.
Il fattore principale di cui occorre tener conto è quello della lunghezza delle canna in quanto, specie nelle armi corte, la velocità reale del proiettile può essere di gran lunga inferiore a quella che ci si potrebbe attendere leggendo i dati delle case produttrici. Nei revolver inoltre è necessario tener conto della perdita di pressione dovuta alla maggior o minor fuga di gas fra tamburo e canna (in termini di energia, la perdita può variare dal 10 al 20%).
La variazione di velocità dipendente dal variare della lunghezza della canna, naturalmente entro limiti ragionevoli (per una pistola non avrebbe senso una canna lunga meno di 4 cm o più di 40 cm), può essere calcolata in modo alquanto approssimativo assumendo che la variazione di velocità sia proporzionale alla radice quarta degli spazi percorsi dai proiettili nelle rispettive canne. Lo spazio percorso si calcola misurando la lunghezza che intercorre tra la punta del proiettile e la bocca della canna, aggiungendo poi ad essa la lunghezza del proiettile. Si avrà quindi

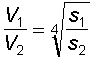
Se, ad esempio un proiettile di pistola sviluppa 320 m/s in una canna di 15 cm., in una canna di 5 cm la velocità sarà di

Risultati molto più precisi possono ottenersi se si tiene conto anche della progressività della polvere individuata in base ad una costante. Questa può essere ricavata dalla velocità iniziale del proiettile se si conosce il peso della polvere e la lunghezza della canna.
Sia:
S = percorso del proiettile in mm nella canna, misurato dalla base del proiettile nella cartuccia alla bocca dell'arma.
C = calibro in mm
P = peso del proiettile in gr
M = peso della polvere il gr
R = costante di progressività della polvere
La balistica interna ci insegna che la velocità del proiettile sarà data dalla formula (Weigel)

da cui si ricava che

Stabilita per una determinata cartuccia e una certa lunghezza di canna, la velocità iniziale del proiettile e quindi il valore di R, sarà facile calcolare la velocità per una diversa lunghezza di canna o per una diversa carica, introducendo il valore di R nella penultima formula. Ho predisposto un programma da scaricare e che esegue questo calcolo.
Si prenda ad esempio un proiettile cal 9 Para con palla di gr. 7,5 e carica di polvere di 0,26 gr, che sviluppa una velocità iniziale di 332 m/s e supponiamo che sia stato sparato in una canna di 120 mm con un percorso del proiettile pari a 105 mm e senza perdite di gas. La costante R sarà pari a 1716. Se ora assumiamo di impiegare una canna di 80 mm, con un percorso libero del proiettile pari a 65 mm, ed inseriamo questi due valori nella formula di Weigel, otterremo che la velocità iniziale si sarà ridotta a 294 m/s.

TABELLA I dei fattori di Heydenreich

         A	     B	      C	         D         F
0.25     0.0313     0.139     0.324     0.216     0.725
0.26     0.0330     0.146     0.326     0.220     0.732
0.27     0.0347     0.152     0.327     0.226     0.740
0.28     0.0365     0.159     0.329     0.231     0.747
0.29     0.0383     0.165     0.331     0.237     0.755
0.30     0.0402     0.172     0.333     0.242     0.762
0.31     0.0421     0.178     0.335     0.250     0.770
0.32     0.0440     0.186     0.337     0.256     0.777
0.33     0.0460     0.193     0.339     0.263     0.785
0.34     0.0480     0.200     0.341     0.269     0.792
0.35     0.0500     0.207     0.343     0.278     0.800
0.36     0.0521     0.214     0.345     0.282     0.807
0.37     0.0542     0.222     0.347     0.288     0.814
0.38     0.0563     0.229     0.350     0.294     0.822
0.39     0.0585     0.237     0.351     0.300     0.829
0.40     0.0608     0.244     0.354     0.304     0.836
0.41     0.0631     0.252     0.356     0.313     0.844
0.42     0.0654     0.260     0.359     0.319     0.851
0.43     0.0678     0.268     0.361     0.325     0.858
0.44     0.0703     0.276     0.364     0.332     0.866
0.45     0.0729     0.284     0.366     0.340     0.873
0.46     0.0756     0.292     0.369     0.346     0.880
0.47     0.0784     0.301     0.371     0.354     0.888
0.48     0.0813     0.309     0.374     0.363     0.895
0.49     0.0843     0.318     0.377     0.372     0.902
0.50     0.0875     0.326     0.380     0.382     0.910
0.51     0.0908     0.335     0.383     0.394     0.918
0.52     0.0944     0.343     0.386     0.407     0.926
0.53     0.0981     0.352     0.390     0.421     0.934
0.54     0.1020     0.361     0.393     0.437     0.942
0.55     0.1061     0.370     0.396     0.454     0.950
0.56     0.1099     0.379     0.399     0.470     0.958
0.57     0.1141     0.388     0.403     0.487     0.966
0.58     0.1185     0.397     0.406     0.505     0.974
0.59     0.1230     0.406     0.409     0.524     0.983
  

TABELLA 2 dei fattori di Heidenreich

         G         H         J
0.25     0.741     0.392     0.610
0.50     0.912     0.635     0.780
0.75     0.980     0.834     0.903
1.00     1.000     1.000     1.000
1.25     0.989     1.130     1.081
1.50     0.965     1.262     1.154
1.75     0.932     1.366     1.219
2.00     0.898     1.468     1.282
2.50     0.823     1.632     1.394
3.00     0.747     1.763     1.495
3.50     0.675     1.875     1.589
4.00     0.604     1.983     1.682
4.50     0.546     2.068     1.769
5.00     0.495     2.140     1.851
6.00     0.403     2.269     2.012
7.00     0.338     2.363     2.163
8.00     0.284     2.445     2.309
9.00     0.248     2.509     2.451
10.00    0.220     2.566     2.589
11.00    0.199     2.615     2.725
12.00    0.181     2.659     2.858
13.00    0.164     2.702     2.988
14.00    0.150     2.740     3.116
15.00    0.137     2.777     3.253
16.00    0.125     2.811     3.390
17.00    0.117     2.837     3.502
18.00    0.109     2.862     3.618
19.00    0.102     2.887     3.740
20.00    0.096     2.910     3.816
25.00    0.073     3 003     4 455
30.00    0.058     3.075     5.031
35.00    0.048     3.162     5.657
40.00    0.041     3.223     6.261
  

email - Edoardo Mori	top

Sitemap: in Italiano | auf Deutsch | in English |

http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003