
 |
| back |
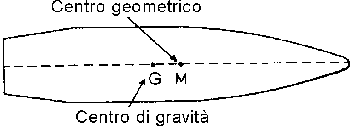
Nel proiettile a corpo cilindrico il centro di gravità è spostato all'indietro rispetto al centro geometrico del proiettile, il che ha come conseguenza che esso sarà sbilanciato all'indietro; mentre il baricentro segue la traiettoria, nella tangente ad ogni suo punto, l'asse del proiettile formerà un certo angolo con la tangente; vale a dire che la punta del proiettile viene a trovarsi sopra la traiettoria e non è diretto con precisione verso il bersaglio.
Altra conseguenza della forma del proiettile è che il punto di incidenza della resistenza dell'aria non cade sul baricentro, ma su di un altro punto, tra esso e la punta del proiettile; in un proiettile allungato e appuntito questo punto sarà più spostato in avanti; in uno tozzo sarà più spostato verso il baricentro. Un corpo cilindrico lungo comporterà poi un ulteriore arretramento di questo punto. In via generale si può affermare che la differenza tra baricentro e punto di attacco è tanto più grande (o piccola) quanto più lungo (o corto) è il proiettile oppure quanto più piccola (o grande) la sua densità sezionale. L'entità di questa differenza è molto importante.
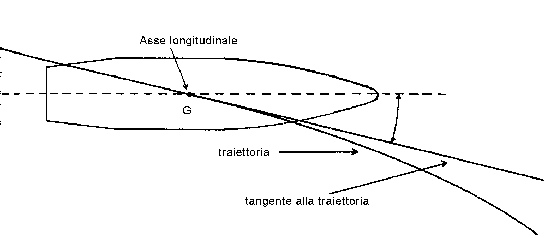
Il fatto che l'asse nel proiettile non coincida con la tangente alla traiettoria comporta che l'aria incide sul proiettile con una spinta che agisce dal di sotto sulla punta del proiettile e tende a rovesciarlo; quanto maggiore detta differenza oppure quanto maggiore la velocità, tanto maggiore sarà il momento rotatorio tendente a rovesciare il proiettile. Anche una rigatura troppo profonda sul proiettile o il suo profilo anteriore tagliente (privo di ogni significato pratico, ma amato dai cacciatori) spostano negativamente il punto di applicazione della resistenza dell'aria.
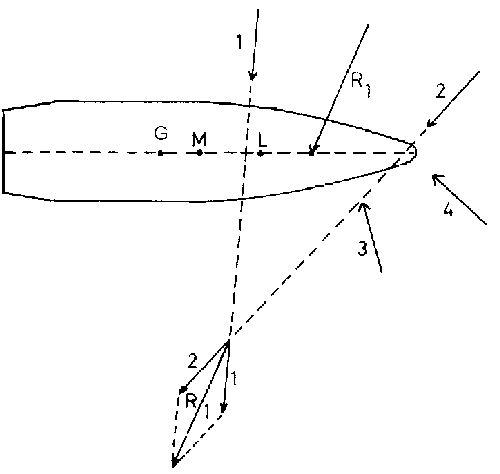
La soluzione a questo problema sta nella stabilizzazione del proiettile mediante la rigatura della canna oppure mediante sua impennatura.
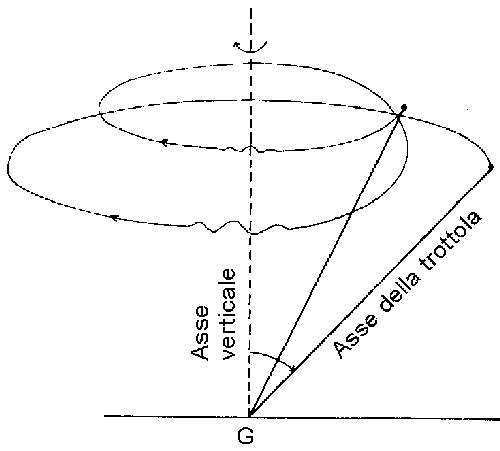
La rigatura ha l'effetto di trasformare il proiettili in un sistema giroscopico (in una trottola per usare termini più alla mano). Chi ha osservato una trottola avrà notato le caratteristiche del suo movimento: 1) il suo asse verticale tende a deviare sempre di più dalla perpendicolare; 2) la punta della trottola percorre sul piano delle lente spirali; dopo un po' di tempo la trottola inizia ad oscillare vistosamente, la sua velocità di rotazione diminuisce per effetto dell'attrito e alla fine cade e si ferma. In una trottola sofisticata come un giroscopio si ha lo stesso comportamento, che talvolta sembra contraddire alle leggi della fisica: se il giroscopio in movimento viene sospeso con l'asse orizzontale invece che verticale, esso continua a ruotare in quella posizione. Non è questa la sede per fornire la spiegazione teorica dei movimenti giroscopici; giungiamo subito alla conclusione secondo cui un corpo in rapida rotazione, e quindi un proiettile, è soggetto a due movimenti: 1) la rotazione lungo l'asse longitudinale che in parte riduce l'effetto della forza di gravità e impedisce lo spostamento dell'asse; 2) spostamento dell'asse in direzione del movimento di rotazione (precessione; l'asse descrive una superficie conica); 3) spostamento dell'asse, anche per effetto della forza di gravità, che produce cicloidi o oscillazioni che si sovrappongono al movimento di precessione (nutazioni).
Il proiettile si differenzia un po' dal giroscopio per il fatto che il punto di rotazione è il centro di gravità e che tutto il sistema si sposta in avanti; sul proiettile quindi la forza che maggiormente agisce è la resistenza dell'aria. Se è nota la forza di gravità e la grandezza del momento di rotazione, si può stabilire l'entità del movimento di precessione.
Siccome asse del proiettile e tangente alla traiettoria non sono congruenti, ma formano un angolo, i movimenti di precessione e nutazione avranno luogo attorno alla tangente.
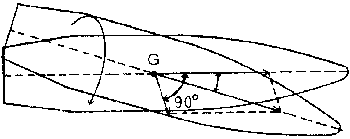
Inoltre il movimento di nutazione nel proiettile si verifica solo periodicamente perché viene attenuato dalla resistenza dell'aria; in realtà infatti i vari movimenti si sovrappongono, talvolta attenuandosi, talvolta sommandosi; i fattori che intervengono sono numerosissimi (si pensi alla enorme varietà di forme e misure dei proiettili) e accertabili solo in via sperimentale e non è facile descriverli neppure con complicatissima analisi matematica. Ed in effetti gli esperimenti compiuti per verificare la stabilità dei proiettili sono molto scarsi (cartucce militari M1 ed M2).
Il compito della rigatura di un arma è quello di impedire che il proiettile si capovolga e di fa sì che il suo asse longitudinale rimanga il più possibile aderente alla tangente alla traiettoria. Quanto meno si raggiunge questo risultato e tanto più si ha un aumento di pressione dell'aria sul proiettile dal lato verso la tangente e che spinge il proiettile nella direzione della rigatura (effetto Poisson) e ad allontanarsi ulteriormente dalla tangente. Questa deviazione viene indicata come "deviazione dalla condizione di equilibrio" o "punto zero" ed è costante, a parità di rigatura, per un determinato proiettile e una data lunghezza di canna. Esperimenti compiuti dai Ballistic Research Laboratories di Aberdeen hanno indicato che a 1000 metri di distanza è circa di 30 cm in orizzontale e 3 cm in verticale. Questa deviazione viene compensata in sede di taratura dell'arma.
Constatato così che i fenomeni fisici che intervengono su di un proiettile sono talmente numerosi e reciprocamente intricati, così che è vano cercare di trovare una regola semplice che possa guidare nel calcolare la stabilità di un proiettile, vediamo almeno di individuare alcuni criteri generali che posano almeno servire da guida.

Ferme restando le altre condizioni si può affermare che
1) L'ampiezza di precessione e nutazione sono proporzionali alla velocità di rotazione del proiettile;
2) La velocità di rotazione varia in funzione del passo di rigatura e della velocità del proiettile; ciò significa che la precisione intrinseca di un proiettile varia con la sua velocità o, espresso altrimenti, se in una stessa arma si varia la velocità del proiettile, varia in modo corrispondente la sua dispersione nella rosata.
3) Se un proiettile viene sparato alla stessa velocità iniziale da canne con diverso passo di rigatura, si ottiene la miglior concentrazione della rosata solo con una determinata combinazione.
4) In conclusione: la stabilità e la coerenza di un dato proiettile aumentano o diminuiscono se cambia la sua velocità di rotazione.
In termini matematici la stabilità si esprime con la formula (1)
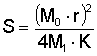
in cui M0 è il momento di inerzia del proiettile lungo l'asse longitudinale, M1 è il momento di inerzia lungo l'asse perpendicolare al precedente e passante per il centro di gravità, r è la velocità angolare di rotazione e K un fattore che vedremo.
Posto f= frequenza di rotazione e p = passo di rigatura, la velocità di rotazione è data dalla formula 6,28 · f ed f da V0 /p e quindi (2)
Un proiettile con velocità di 1000 ms sparato da una canna con passo di 0,25 rotazioni per metro avrebbe quindi all'uscita dalla canna una frequenza di 4000 giri al secondo e una velocità di rotazione pari a 6,28 · 4000.
Dalla formula 2 si ricava che la stessa velocità di rotazione può ottenersi con diverse combinazioni di velocità iniziale e di passo. Perciò se per stabilizzare un proiettile che viaggia ad 800 ms è richiesta una frequenza di 4000 giri al secondo, il passo dovrà essere di 0,20 giri al metro.
Il momento di inerzia del proiettile lungo l'asse longitudinale è dato dall'integrale (3)
![]()
in cui k indica il raggio del calibro e m la massa del proiettile così che può scriversi (4)
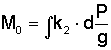
in cui P è il peso e g la gravità.
Questa formula ci dice che il momento d'inerzia è direttamente proporzionale al peso del proiettile e che varia in misura quadratica rispetto al calibro, ragione per cui l'influenza del calibro è rilevante. In pratica ciò significa che se per un certo proiettile è richiesto un certo momento di inerzia, il proiettile dovrà avere un dato peso; se si diminuisce il calibro si dovrà aumentare il peso del proiettile.
Il momento di inerzia dell'asse perpendicolare è espresso dalla stessa formula (4) in cui invece di k si inserisca h² che indica la distanza fra punto di incidenza della resistenza dell'aria e centro di gravità. Questa varia a seconda del fattore di forma i e della lunghezza del proiettile l.
Il fattore K varia in funzione della velocità, del peso, della distanza h e del coefficiente balistico, così che si può scrivere la formula (in cui delta = densità dell'aria)
(5)K = V · h · i · k² · delta
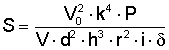
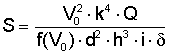
La formula, troppo approssimativa, non serve per il calcolo preciso della stabilità, ma per indicare la relazione fra i vari fattori in gioco.
Secondo l'opinione comune un proiettile si considera sufficientemente stabilizzato quando S è maggiore di 1 in quanto si riduce al minimo l'effetto di "sfarfallio" dovuto alla nutazione. Quanto maggiore il fattore S, tanto maggiore è l'ammortizzazione della nutazione. Nella pratica si è trovato che il valore ottimale è da 1,3 ad 1,8.
Ripetiamo quindi che il valore di S diventa tanto più grande (o piccolo) quanto più grande (o piccolo) è il denominatore nella frazione (7); la velocità di rotazione cresce (o cala) in rapporto diretto con la velocità alla bocca e in rapporto inverso con il passo della rigatura.
Esaminando ulteriormente i valori della formula (7) si vede che un aumento della velocità iniziale influisce senz'altro sulla stabilizzazione in quanto la velocità entra nel dividendo al quadrato; la stabilità diminuisce via via che cala la velocità del proiettile, fino a che si arriva ad una velocità critica al di sotto della quale la stabilità non è più sicura.
Il passo entra nella formula al quadrato, ma nel divisore: perciò una diminuzione del passo aumenta notevolmente la stabilità. Dal fatto che il raggio del calibro entri nella formula alla quarta potenza mentre la densità sezionale vi compare in forma semplice, si può dedurre che proiettili di grosso calibro e corti sono meglio stabilizzati di proiettili di piccolo calibro e lunghi (ovviamente si trascurano qui altri aspetti, quali la diversa resistenza dell'aria e il diverso comportamento la vento laterale, che rendono consigliabili una buona densità sezionale).
Il fattore di forma i e la distanza h (essa pure influenzato da i) alla terza potenza, ci dicono che fra due proiettili dello stesso speso ma di calibro diverso, è più stabile quello con la punta più slanciata; se di peso diverso ma con punta eguale, quello con la minor densità sezionale; se di peso eguale ma di calibro diverso quello con il calibro maggiore.
La coerenza (ingl. tractability) di un proiettile
Per coerenza del proiettile si intende quella caratteristica per cui il suo asse segue la direzione del movimento (tangente alla traiettoria); sua caratteristica è che l'angolo tra asse e tangente deve restare piccolo in ogni punto della traiettoria. Il che si ha quando la variazione di questo angolo è sempre minore della variazione dell'angolo di precessione.
Il quoziente di questi due angoli si chiama fattore di coerenza e può essere descritto dalla formula (8)
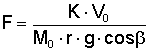
in cui cosβ (coseno beta)indica il coseno dell'angolo della tangente alla traiettoria (angolo fra tangente e orizzonte) che varia continuamente durante il volo del proiettile e che quindi assume valori da positivi a negativi. La formula si può semplificare per il vertice della traiettoria in cui il valore è eguale a 1 e si può scrivere la (9)
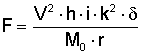
Confrontando le formule (7) e (9) si vede che al variare del momento di inerzia o del calibro, S ed F variano in direzione opposta; il che significa che un massimo di coerenza si ottiene con un valore minimo di stabilità, e viceversa, così che è necessario trovare un compromesso tra i due valori. Ma quale dei due è il più importante?
La coerenza ci dice di quanto l'asse longitudinale del proiettile è allineato alla tangente alla traiettoria. Una grande (/piccola) coerenza comporta, tra l'altro una minore (/maggiore) deviazione dalla situazione di equilibrio. Però questa deviazione è praticamente priva di significato per le armi leggere in cui viene corretta con la taratura.
La stabilità per contro ci indica la misura delle oscillazioni del proiettile a causa della nutazione e quindi la dispersione sul bersaglio ed è indubbiamente più importante della coerenza nelle armi leggere, essa garantisce la precisione intrinseca del singolo proiettile.
Si può perciò concludere che in pratica: la precisione intrinseca di un proiettile è tanto più grande (/piccola) quanto più grande (/piccolo) è il suo calibro, quanto minore (/maggiore) il passo, quanto maggiore (/minore) la sua velocità iniziale, quanto minore (/maggiore) il fattore di forma, quanto minore (/maggiore) la sua lunghezza.
Per tale motivo per una carabina con un canna avente un dato passo di rigatura vi sono poche combinazioni di componenti di carica che diano una stabilizzazione ottimale e la minor dispersione; combinazioni da trovare con esperimenti pratici.
La formula di Greenhill
È una formula empirica per calcolare il passo di rigatura che è necessario per stabilizzare un proiettile di una data lunghezza. Essa, vecchia di settant'anni, si basa sulla semplice regola che quanto più lungo il proiettile (cioè, ancora più in generale, quanto più pesante per un dato calibro), tanto maggiore deve essere la velocità di rotazione.
La formula è:
T = 150 *(D/R)
In cui T è il passo in pollici (spazio in cui il proiettile compie un giro)
D è il diametro in pollici
R è la lunghezza del proiettile diviso il diametro.
La costante 150 è relativa a velocità di 1500 piedi/secondo (= 450 ms) ; per 2800 p/s (= 850 ms) inserire 180.
Ma se R e eguale L/D, si può scrivere
T= 150 * D2 /L
Sia la lunghezza del proiettile 1,064" (= 27 mm)
Il passo richiesto sarà dato da
T= 150 · 0,2242 / 1,064 = 7,07" di passo (= 17,96 cm)
Si potrebbe calcolare direttamente in mm:
Vediamo ora il calcolo in millimetri
T = 150 · 5,69 · 5,69/27 = 179 mm
Per converso, per trovare la lunghezza del proiettile che una data rigatura può stabilizzare si userà la formula
L = 150 · (D · D/T) o meglio 150 · D2 /T
Dove L è la lunghezza del proiettile.
L = 150 · 5,69 · 5,69/179= 27 mm
Proiettili stabilizzati con impennatura
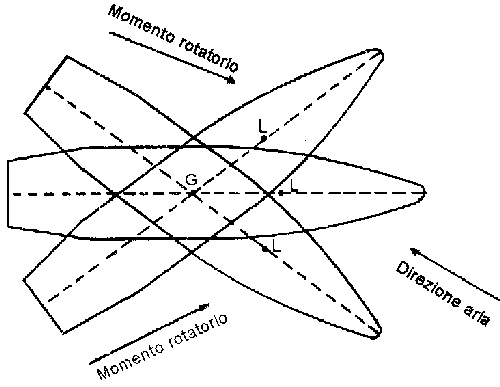
Il loro comportamento si differenzia dai precedenti per il fatto che il loro punto di gravità si trova tra la punta e il punto di incidenza dell'aria sia perché così costruiti con adeguata distribuzione delle masse, sia per alette posteriori che spostando il punto di incidenza all'indietro. Queste alette sono più efficaci se sporgono oltre il calibro del proiettile. È possibile che esse non sporgano, ma allora devono essere alquanto lontane dalla punta del proiettile. Le alette produco una elevata coerenza del proiettile che per tutta la traiettoria ritorna rapidamente a seguire la tangente alla traiettoria.
Questi proiettili non richiedono un movimento rotatorio, ma si è visto che una lieve angolazione delle alette tale da imprimere una rotazione di alcune centinaia di giri al minuto, correggono errori di traiettoria dovuti a scarsa simmetricità. La frequenza di rotazione deve essere stabilita sperimentalmente per evitare che sia vicina a quella dei movimenti pendolari, a cui verrebbe a sommarsi.
Vantaggi: possibilità di proiettili lunghi e quindi con grande densità sezionale; uso di proiettili asimmetrici; possibilità di guidarli in volo; possibilità di trasporto di cariche che non sopportano la forza centrifuga.
Svantaggi: un maggior Cx riferito alla densità sezionale; formazione di vortici alla base del proiettile.
| Sitemap: in Italiano | auf Deutsch | in English | |
| http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003 |