Il rimbalzo dei proiettili

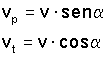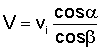
Il rimbalzo dei proiettili segue le normali leggi della fisica. Il proiettile raggiunge una superficie con l'angolo α ed una velocità che si scompone in due componenti, la prima perpendicolare alla superficie e la seconda (tangenziale) parallela alla superficie secondo le formule

Solo la componente verticale agisce sulla superficie e, correlativamente, sul proiettile; perciò con più l'angolo α è piccolo, minori sono questi effetti su superficie e proiettile. Dopo l'urto la componente tangenziale della velocità rimane inalterata (salvo modesta perdita per attrito sulla superficie) mentre la componente verticale si riduce a seconda della elasticità ε dell'urto. Se ε = 0 si ha un urto plastico con completa dispersione nell'energia all'impatto, senza rimbalzo alcuno. 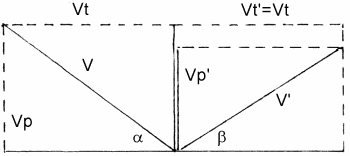Se ε = 1 (biglia di acciaio su piastra di acciaio) la componente verticale della velocità rimane inalterata; se ε < 1 (palla camiciata, ad es.), la componente verticale della velocità assumerà il valore V_p'= V_p · ε e l'angolo di riflessione β sarà minore dell'angolo di incidenza. La velocità con cui il proiettile rimbalza sarà data dalla formula

Ciò significa che in caso di urto molto elastico il proiettile prosegue in una nuova direzione con una velocità prossima a quella di impatto; per effetto dell'urto esso sarà destabilizzato, roteerà vorticosamente con aumento del coefficiente aerodinamico, ma potrà avere pur sempre una gittata pari ad un terzo di quella che avrebbe normalmente.
Gli angoli α e β vanno misurati sperimentalmente. In alcuni casi si risconta che l'angolo β è maggiore dell'angolo α; ovviamente non vengono violate le leggi della fisica, ma accade che il proiettile provochi e percorra nel materiale una breve scanalatura o deformazione che devia il proiettile con un angolo maggiore di quello di impatto. La velocità però non sarà più calcolabile con la formula ora vista.
Con l'aumento dell'angolo α aumenta la componente della velocità d'impatto e la relativa energia con maggior deformazione del proiettile. Per ogni combinazione di proiettile-superficie vi è un angolo α a cui il proiettile o penetra oppure si frammenta, così che rimbalzano sono i frammenti. In alcuni casi può accadere che il proiettile provochi nella superficie un foro più grande del suo calibro, venendo poi però rimbalzato senza passare dall'altra parte (fenomeno frequente su lastre di vetro, ma possibile anche su lastre di metallo, così che poi gli investigatori cercano il proiettile dal lato sbagliato!).
Sia ben chiaro che il valore ε non è fisso per ogni materiale perché dipende dal tipo di proiettile e varia a seconda dello spessore e del montaggio del materiale del bersaglio.
Esperimenti pratici eseguiti su lastre di vari metalli hanno mostrato che si ha rimbalzo fino ad angoli α pari a 40-50° e con un angolo β al di sotto dei 10°.
Con proiettili cal 22 lr il valore di ε è pari a 0,11 per lastre di acciaio di 1,6 mm e a 0,03 per lastre di 3,2 mm. Con proiettili cal. 45 i valori sono rispettivamente 0,29 e 0,078.
Sparando con il cal. 7,65 mm si riscontra che i proiettili iniziano a penetrare con un angolo di 17-22°. Con meno di 17° si ha il fenomeno per cui l'angolo di impatto è minore dell'angolo di rimbalzo. Oltre 35° si ha frammentazione del proiettile.
Il legno ha un comportamento diverso dal metallo e paragonabile a quello dell'acqua; il proiettile non rimbalza come su di una superficie dura, ma penetra nel legno, vi provoca una scanalatura e viene deviato verso l'alto per lo stesso fenomeno per cui un raggio di luce viene deviato passando dall'aria all'acqua (ma intervengono anche fenomeni idrodinamici). La conseguenza è che quanto maggiore è l'angolo α, tanto maggiore diventa l'angolo β, fino a che non si raggiunge l'angolo di impatto (angolo critico) che consente la penetrazione del proiettile. Questo per proiettili sparati su tavole di legno; se si spara nel legno "di punta", cioè su di una sezione orizzontale del tronco, il legno può comportarsi in modo estremamente elastico.
L'angolo critico per proiettili di pistola nel legno di abete è da 10° (9 mm. para) a 15° (cal. 22 e cal. 7,65); per proiettili di fucile è di circa 5°.
L'angolo critico per il vetro è attorno ai 40°, ma si possono avere rimbalzi anche con impatti di 60 °. Sul cemento si hanno valori di 30-40° gradi, molto variabili a seconda del tipo di cemento e di proiettile.
I proiettili rimbalzano anche sulla sabbia con un angolo critico di circa 10° (circa 20° per gli slug).
Sull'acqua l'angolo critico è di circa 5-7° l'angolo β è di poco inferiore e, talvolta, superiore.
Difficili da prevedere e da calcolare sono i rimbalzi e le deviazioni contro superfici curve (ad esempio tronchi o rami).
Secondo esperimenti dello FBI uno sparatore in piedi che spara a 23 metri (25 yarde) sul terreno coperto di asfalto o cemento (angolo 3,5°), con la pistola, può colpire alle gambe o al basso ventre una persona che si trovi a 50 yd; sull'erba oppure con palla slug lo può colpire al petto.