La probabilità di colpire

Il calcolo delle probabilità consente di calcolare quante probabilità vi sono che un evento possibile, ma non certo, si verifichi.
La probabilità P che un evento si verifichi è data dal rapporto tra eventi favorevoli ed eventi possibili: la probabilità che esca il sei lanciando un dado una sola volta è data da P = 1/6 = 0,166 dal che si ricava che il valore di P non può mai essere superiore ad uno, poiché in tal caso si ha la certezza che l'evento si verifichi.
La probabilità che l'evento non si verifichi sarà evidentemente data da 1-P
La probabilità che si verifichino contemporaneamente un certo numero di eventi indipendenti l'uno dall'altro è pari al prodotto della probabilità di ciascun evento. Se la probabilità di colpire un bersaglio è P = 0,1 la probabilità di colpirlo due volte di seguito sarà P · P = 0,01 Viceversa la probabilità di non colpirlo due volte di seguito sarà data da P = (1 - 0,1) · (1 - 0,1) = 0,89 e così via.
Diverso è naturalmente il problema di stabilire quante probabilità si avrebbero di colpire il bersaglio almeno una volta sparando 5 colpi. Passaggi un po' complicati portano alla formula P = 1 - (1 - 0,1)elevato alla quinta = 0,4 Se la probabilità di colpire varia ad ogni colpo, ad esempio da 0,1 a 0,15 a 0,2, ecc. (si pensi ad un bersaglio che si avvicina sempre più al tiratore!), la formula diventa P = 1 - (1 - 01) · (1 - 0,15) · (1 - 2) ....

Per eseguire calcoli di questo tipo occorre perciò apprendere come calcolare il valore di P, cosa abbastanza facile.
Ogni arma a palla, anche se provata al banco, non è in grado di concentrare i proiettili in un unico punto, ma li disperde attorno al punto mirato entro un'area di dispersione che possiamo assumere come circolare. Se il centro del bersaglio e il centro del circolo di dispersione non coincidono, ciò significa che vi è un difetto da correggere nel sistema di puntamento.
La dispersione naturalmente aumenta, in modo poco più che proporzionale, con l'aumentare della distanza dell'arma dal bersaglio; aumenta inoltre quando al fattore meccanico si aggiunge quello umano: ogni tiratore, a seconda della sua abilità, del suo stato psicofisico, a seconda delle circostanz ambientali, concentrerà più o meno i colpi sul bersaglio.
Questa dispersione del tiro può essere valutata con metodi statistici.
Di norma lo studio della dispersione del tiro con artiglierie sul terreno, e quindi rispetto a bersagli orizzontali, in cui i tiri presentano una dispersione ellittica, essendo la dispersione maggiore in lunghezza che in larghezza. Noi invece ci vogliamo occupare solo del tiro contro bersagli verticali ove la dispersione, come si è detto, può ritenersi circolare e quindi sarà sufficiente, per i successivi calcoli, di individuare lo scarto quadratico medio dei singoli proiettili rispetto al centro della rosata.
Supponiamo di avere sparato dieci colpi contro un bersaglio e di aver ottenuto la rosata di figura 1.

Figura 1

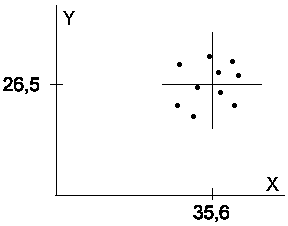
Per prima cosa occorre individuare il centro medio della rosata. Ciò si può ottenere in modo empirico tracciando prima un asse orizzontale in modo che vi siano metà dei colpi sopra e metà dei colpi sotto di esso, e poi un asse perpendicolare al primo che lasci metà dei colpi a sinistra e metà dei colpi a destra: il punto d'incontro rappresenta il centro ideale della rosata.
Per calcolare ora lo scarto quadratico medio, vale a dire la media dei quadrati delle deviazioni di ogni singolo colpo dal centro medio, occorre misurare la distanza di ogni colpo dal centro medio ed elevare il valore trovato al quadrato. La radice quadrata della media dei valori così trovati ci darà il valore M ricercato.
Invece di misurare la distanza dal centro ideale di ogni colpo, si può, più semplicemente, come nell'esempio di figura 1, calcolare lo scarto di ogni valore di X e di Y rispetto al valore X-Y del centro medio e poi estrarre la radice quadrata della somma dei loro quadrati, con normale applicazione del teorema di Pitagora.
Nell'esempio si avrebbe che le coordinate del centro medio sono X = 35,6 e Y = 26,5 e che le coordinate dei singoli colpi, la differenza D dal valore medio, i loro quadrati, avrebbero i seguenti valori:

 X   D     D²     Y    D     D²
32  3,6  12,96    19  7,5  56,25
41  5,4  29,16    21  5,5  30,25
33  2,6   6,76    26  0,5   0,25
42  6,4  40,96    28  1,5   2,25
28  7,6  57,76    31  4,5  20,25
36  0,4   0,16    33  6,5  42,25
28  7,6  57,76    22  4,5  20,25
37  1,4   1,96    24  2,5   6,25
41  5,4  29,16    32  5,5  30,25
38  2,4   5,76    29  2,5   6,25 
356      242,4   265        214,5

da cui si ricava direttamente lo scarto quadratico medio per X = 24,24 e per Y = 21,45.
Il valore di M sarà infatti dato dalla radice quadrata della somma (24,24 + 21,45) = 6,76 cm (manca il segno di radice!) Il valore così trovato consente di determinare il parametro più importante di tutta la teoria del tiro e cioè lo scarto probabile S.

Per comprenderne il significato si pensi ad un'arma che spara una serie di colpi dal punto O in direzione OX

                                   B
          O -----------------|-----|----|------X
                                a     a

Il punto medio di caduta sia B; se si prendono in esame due strisce di terreno prima e dopo il punto B e se a è piccolo, in esse si riscontrano pochi colpi e quindi la probabilità di colpire quella striscia è piccola e la maggior parte dei colpi cadrà fuori di essa. Per un certo valore di a vi saranno tanti colpi fuori della striscia quanti entro di essa. A questo punto la probabilità che un proiettile cada entro la striscia è pari a 0,5 e cioè ad un colpo su due. Questo valore a corrisponde al parametro S e il valore 2S indica la larghezza di una striscia di terreno posta simmetricamente a lato del punto medio e che ricomprende la metà dei colpi sparati che si trovano più vicini al punto medio, la metà dei punti migliori.
Se il ragionamento, invece che alla sola dispersione longitudinale sul terreno viene riferita alla dispersione in altezza e in larghezza su di un bersaglio verticale, si otterrà che se nella larghezza 2S cade il 50% dei colpi, in un quadrato ne cadrà lo 0,5x 0,5 e cioè lo 0,25%; in un cerchio infine avente il raggio S, ricadrà il 20% circa dei colpi (il cerchio iscritto in un quadrato ha una superficie inferiore di circa 1/5 a quella del quadrato stesso).
Il valore di S che, nel caso sia calcolato per una dispersione unidimesionale, è dato dalla formula S = 0,6745M, nel caso di una superficie è dato dalla formula S = 0,4769M.
Nel caso della figura 1 si avrebbe perciò S = 6,76 x 0.4769 = 3,22 cm.

Il calcolo della distribuzione dei colpi all'interno di un cerchio, stabilito il valore di S, è un po' complicato in quanto occorre far riferimento ad un valore di P dato dalla funzione

in cui K = Raggio/S ed e = 2,718.

Più semplicemente il valore di P in funzione del valore K può essere ricavato dalla seguente tabella.

 K       P           K       P           K       P   
0,1    0,002        2,1    0,633        4,1    0,978
0,2    0,009        2,2    0,667        4,2    0,982
0,3    0,020        2,3    0,700        4,3    0,985
0,4    0,036        2,4    0,730        4,4    0,988
0,5    0,056        2,5    0,759        4,5    0,990
0,6    0,079        2,6    0,785        4,6    0,9919
0,7    0,106        2,7    0,810        4,7    0,9934
0,8    0,136        2,8    0,832        4,8    0,9947
0,9    0,168        2,9    0,852        4,9    0,9958
1      0,203        3      0,871        5      0,9966
1,1    0,240        3,1    0,888        5,1    0,9973
1,2    0,279        3,2    0,903        5,2    0,9979
1,3    0,319        3,3    0,916        5,3    0,9983
1,4    0,360        3,4    0,928        5,4    0,9987
1,5    0,401        3,5    0,938        5,5    0,9990
1,6    0,441        3,6    0,948        5,6    0,9992
1,7    0,482        3,7    0,956        5,7    0,9994
1,8    0,521        3,8    0,963        5,8    0,9995
1,9    0,560        3,9    0,969        5,9    0,9996
2      0,597        4      0,974        6      0,9997

Dalla tabella si vede che per R = S e quindi K = 1, un cerchio con raggio eguale ad S contiene il 20,3% dei colpi; un cerchio con raggio pari a 2S, e quindi con K = 2, il 59,7% dei colpi, e così via.
Per contro dalla tabella si legge che il cerchio avente una probabilità del 50% di essere colpito, si ottiene moltiplicando S per un valore K di circa 1,75 (che si ottiene mediante interpolazione tra 0,482 e 0,521) e quello con probabilità del 75% moltiplicandolo per 2,47.

Si potranno quindi risolvere i seguenti problemi relativi a bersagli circolari.
1) Quale raggio ha il cerchio che contiene il 50% e il 75% dei colpi, data la rosata di figura 1?
Soluzione:
R(50) = 1,7456 · S = 1,4756 · 3,22 = 5,62 cm
R(75) = 2,4686 · S = 2,4686 · 3,22 = 7,95 cm

2) Con una pistola sono stati sparati numerosi colpi contro un bersaglio con 10 zone (anelli) aventi raggio 4, 8, 12, 16, 20, 24, 28, 36, 40 cm. e si è contato che entro il cerchio di 20 cm è caduto circa il 60% dei colpi. Quale è il valore di S e quale percentuale di colpi è caduta nei singoli cerchi?
Soluzione:
Dalla tabella si vede che per P = 60 si ha K = 2; il valore di S sarà dato dal rapporto R/K e quindi da 20/2 = 10 cm. Si procederà poi al calcolo di K per i vari raggi e da esso a quello delle relative percentuali; le percentuali dei singoli anelli si otterranno poi per differenza.

3) Nel problema n. 2 si voglia stabilire la percentuale di colpi in un determinato anello del bersaglio.
Soluzione:
Sarà sufficiente determinare la percentuale relativa ai due cerchi che delimitano l'anello e fare la differenza. Se, ad esempio, il cerchio interno ha raggio R = 3S e quello esterno R = 4S, si ricava che la percentuale sarà data da 97,4% - 81,7% = 10,3%.
Se occorre conoscere la percentuale di colpi in un solo settore del cerchio o dell'anello, sarà sufficiente dividere i risultati trovati per il rapporto tra cerchio e settore; se, ad esempio, il settore è sotteso da un arco di 36º la percentuale dei colpi ad esso relativa sarà di 1/10 di quella calcolata per il cerchio di 360º.

4) Se S = 4 cm quale percentuale di colpi contiene un cerchio con raggio 10 cm ?
Soluzione:
K sarà eguale a 10/4 e cioè 2,5 da cui si ricava P = 0,75%, vale a dire che un colpo su 4 uscirà dal cerchio.
Si osserva in proposito che conoscendo la percentuale di colpi all'interno di un determinato cerchio, si può direttamente calcolare S senza dover misurare i singoli scarti di ogni colpo; dalla percentuale infatti si risale a K e il rapporto R/K ci darà il valore di S. Ancora più semplicemente si potrà tracciare il cerchio contenente il 20% dei colpi per ottenere R = S.

In molti casi però il tiratore si trova di fronte non figure geometriche quali il bersaglio da tiro a segno, ma figure irregolari e asimmetriche, come la sagoma di un veicolo o di un uomo, rispetto a cui non è facile eseguire il calcolo matematico sopra esposto.
In tali casi si ricorre alla cosiddetta «rete di dispersione di Gauss» illustrata in figura 2,

Figura 2

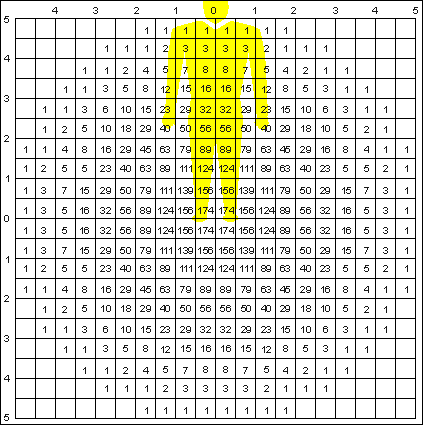
la quale consiste di un quadrato di lato pari a 10S, suddiviso in quadratini aventi lato 0,5S, per ciascuno dei quali è calcolata la percentuale di probabilità di colpirlo (i valori indicati in ogni quadratino vanno divisi per 100!). Se la probabilità di colpire una striscia orizzontale o verticale, non limitata in lunghezza e larga 0,5S, è pari, ad esempio al 13,2% (vedi strisce centrali), la probabilità di colpire il quadrato formato dal loro incrocio sarà dato, secondo le regole del calcolo della probabilità nell'ipotesi di più eventi indipendenti, da 13,2 · 13.2 = 1,74%, come per l'appunto sta scritto nei quadratini centrali.
Per calcolare la probabilità di colpire un determinato bersaglio, sarà quindi sufficiente disegnare la sagome del bersaglio nella stessa scala usata per la rete di Gauss (in figura, usando carta millimetrata, 1 cm = 0,5S) e poi sovrapporre la sagoma facendo coincidere il suo centro con il centro della rete. La somma delle percentuali dei quadratini coperti darà la percentuale di probabilità di colpire quel bersaglio. Se la sagoma copre un quadratino solo in parte, il valore di esso verrà ridotto percentualmente.
Se poi la sagoma viene spostata di un lato di un certo numero di quadratini, si otterrà la percentuale di probabilità per il caso in cui il centro medio della rosata sia spostato rispetto al centro del bersaglio. Per conoscere infine verso quale punto del bersaglio irregolare occorre mirare per ottenere la massima probabilità di colpirlo, bisognerà procedere per tentativi, spostando la sagoma sulla rete fino ad ottenere il valore massimo di probabilità.

Il metodo esposto consente di risolvere eleganti problemi di un certo interesse per la balistica giudiziaria (anche se i giudici hanno bisogno di certezze e non di probabilità).

Accade abbastanza spesso che il feritore di una persona affermi di aver sparato ai piedi della stessa oppure di lato e di averla colpita in punti vitali per sbaglio; il calcolo delle probabilità consente di valutare l'attendibilità della dichiarazione, specialmente quando l'arma presenta una notevole dispersione dei colpi. In alcuni casi si potrebbe tenere conto anche della abilità nel tiro dello sparatore, ma bisognerebbe avere la certezza che egli durante le prove di tiro spari effettivamente secondo le sue possibilità.
Per risolvere il quesito si procederà quindi a determinare il valore di S dell'arma (o del tiratore) alla distanza del caso e si abbia, ad esempio, che a 50 metri S = 30 cm.
Allora ogni lato di un quadratino corrisponderà a 15 cm e, per una sagoma umana di normale corporatura, si potrà disegnare il contorno come in figura. Se lo sparatore afferma di aver sparato ai piedi della vittima, la sagoma andrà sovrapposta sulla rete il modo che il centro della rete si trovi in corrispondenza dei piedi. La probabilità di colpire il corpo al tronco sarà data dalla somma dei valori dei quadratini coperti dal tronco e cioè 0,32 + 0,32 + 0,16 + 0,16 + 0,08 + 0,08 + 0,03 + 0,03 .... ecc. con i quadratini coperti parzialmente, ottenendosi una percentuale di circa 1,4%; vale a dire che su 100 colpi sparati in quelle condizioni solo 1 o 2 potevano colpire il tronco nonostante che lo sparatore avesse mirato ai piedi. Quindi la versione dello sparatore è appena accettabile. Se invece la vittima fosse stata raggiunta al capo, la probabilità di colpirlo scenderebbe a meno dello 0,01%, decisamente inverosimile.

La validità del metodo trova conferma eseguendo il calcolo in via puramente matematica. A tal fine inseriamo la sagoma, come in figura 3, in un settore di anello circolare, usando una scala per cui sia S=30 cm. Il valore ricavato è anche in questo caso pari allo 1,4%.

Figura 3

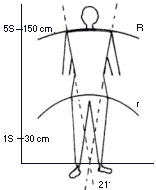
Raggio  R = 150 cm
Raggio  r = 75 cm
KR = 150 : 30 = 5
Kr =  75 : 30 = 2,5
P5 = 99,66
P2,5 = 75,90
99,66 - 75,90 = 23,97%
360 : 21º = 17
23,97 : 17  = 1,4%

La precisione del calcolo della probabilità dipende dalla precisione con cui è stato calcolato il valore S, precisione che più aumenta quanto più ampia la serie di colpi sparati. Affinché i risultati però non risultino falsati da tiri anormali occorre escludere dalle serie di colpi quelli cosiddetti anomali, cioè quelli che per imprevedibili fattori (errore del tiratore, difetto della carica o del proiettile, ecc.) si discostano da quelli che derivano invece dalle normali irregolarità del tiro.
In via approssimativa si considera anomalo quel colpo che in una serie di colpi non supe-riore a 10 ha uno scarto superiore a 5S e, in una serie superiore a 10 colpi, ha uno scarto superiore a 6S.

Un calcolo più preciso può farsi usando il fattore di anomalia di Chauvenet il cui uso è il seguente.
Prima di tutto si calcola il valore di S sui dati relativi ad un certo numero di colpi sparati, come spiegato all'inizio. Poi si controlla se vi sono scarti il cui valore sia superiore al prodotto di y·S in cui y è il fattore di anomalia di Chauvenet, correlato al numero di colpi sparati, secondo la seguente tabella:

Se ve ne sono, questi sono considerati tiri anomali e vengono esclusi, rifacendosi poi da capo il calcolo di M ed S. Nella rosata di figura 1 si avrebbe, ad esempio, 2,91 x 3,22 = 9,3 cm; siccome nessun colpo ha una distanza maggiore dal centro della rosata, vuol dire che non vi sono tiri anomali.


	Home > Balistica > Sottomenu > Documento	back


email - Edoardo Mori	top