Il Pendolo balistico

Per stabilire al velocità di un proiettile non vi è strumento migliore di un cronografo, il cui acquisto è però giustificato solo per chi, come perito balistico o ricaricatore di cartucce, deve ricorrervi di frequente.
Chi invece ha bisogno solo occasionalmente di calcolare la velocità di un proiettile, può ricorrere al vecchio metodo del pendolo balistico, in grado di fornire dati più che attendibili senza alcuna spesa (personalmente ho usato un pendolo fatto con una patata per controllare la velocità di pallini ad aria compressa, e funzionava benissimo).
L'idea di usare un pendolo per determinare la velocità di un proiettile risale a Cassini Junior (1707) e lo strumento derivatone, detto pedolo balistico, venne perfezionato da successivi studiosi (B. Robins, Diddion, Morin, Piobert) ed è stato l'unico ad essere impiegato fino a circa un secolo fa, contribuendo a porre le basi della balistica moderna.
Il principio teorico alla base del pendolo balistico è estremamente semplice: l'arma viene puntata contro una massa pendolare, costituita da materiale atto a trattenere il proiettile ed a realizzare un urto anelastico. Allo sparo quindi il proiettile si conficca nella massa pendolare trasmettendole un impulso; dal teorema della conservazione della quantità di moto e dalle leggi del moto pendolare si deduce la quantità di moto della massa pendolare dall'ampiezza della sua oscillazione, e quindi la velocità del proiettile.
Sia infatti P il peso della massa pendolare e p il peso del proiettile; P+p sarà il peso del pendolo con il proiettile infisso; si poi V la velocità acquisita dal pendolo e v la velocità del proiettile prima dell'urto.
Sarà
p·v = (P+p)·V
da cui
V = (p·v) / (P+p)
Sotto l'influenza dell'urto il pendolo acquista una velocità e quindi una forza viva E, espressa dalla formula

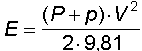
che lo fa alzare di un certo spazio h ove si trasforma in energia potenziale Ep

Ep= (P+p) ·h

Siccome E =Ep, si possono fondere le due espressioni e ricavare che

che è la formula relativa alla caduta dei gravi.
Questo valore dovrà corrispondere a quello derivato dall'impulso e quindi si potrà scrivere:

da cui

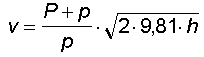
L'altezza h non è misurabile direttamente, ma può essere espressa trigonometricamente in funzione della lunghezza l del pendolo e dell'ampiezza dell' angolo dell'oscillazione secondo la formula
h= l ·(1 - cosã)
(uso per necessità pratiche il simbolo ã per indicare l'angolo alfa)

per cui, in definitiva, la formula da applicare è la seguente

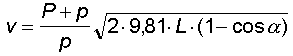
in cui l'unica incognita è data dall'angolo alfa, da misurarsi di volta in volta.
A sua volta, la lunghezza l del pendolo non può essere misurata direttamente poiché ciò che interessa non è la lunghezza effettiva, ma quella riferita al centro di oscillazione del pendolo composto, che si usa in pratica. Essa quindi deve essere determinata indirettamente dalle leggi fisiche del moto pendolare: si determina con un cronometro la durata D in secondi di una oscillazione, contando ad esempio il numero delle oscillazioni compiute in un minuto primo, e da esso si ricava la lunghezza in metri secondo la formula
l = 0,248·D²
Invece di misurare l'ampiezza dell'angolo di oscillazione del pendolo, può essere più semplice misurare l'ampiezza s dell'arco percorso da un suo punto e da essa risalire all'angolo alfa mediante la formula

ove L in questo caso rappresenta la distanza effettiva tra il punto attorno a cui oscilla il pendolo e il punto che traccia l'arco.

Realizzazione pratica

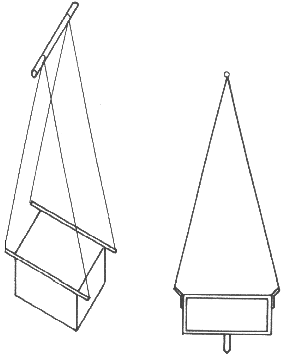
Vediamo ora come si possa costruire praticamente il pendolo.
Esso deve rispondere ai seguenti requisiti:
a) deve avere una lunghezza tale da rendere sufficiente lenta l'oscillazione; la lunghezza L dovrà quindi essere di 1 - 1,5 metri.
b) la massa pendolare deve avere un peso tale non compiere , in relazione al proiettile sparato, una oscillazione superiore a 20° e deve essere sospesa in modo da poter oscillare in un solo piano senza sbandamenti, rotazioni ed oscillazioni parassite. In linea di massima dovrà avere un peso, in grammi, pari al prodotto della velocità del proiettile in m/sec per il suo peso in grammi. Quindi dovrà pesare circa kg 1 per il cal. 22, kg 1,5 per il cal. 7,65 e il cal. 9, e così via.
c) Il blocco deve essere conformato in modo che il proiettile vi penetri e vi resti infisso; per alcuni proiettili sarà sufficiente un blocco di legno, per altri occorrerà provvedere, oltre al legno, degli strati di piombo od altro metallo che impediscano la perforazione completa. In pratica andrà bene qualsiasi scatola metallica, a forma di parallelepipedo o di cilindro, in cui sistemare strati di legno, sabbia, piombo, e sospeso mediante quattro fili sottili e non elastici, riuniti a due a due con anelli , ad un qualunque sostegno stabile.
Al di sotto della scatola, sul prolungamento dell'asse perpendicolare del pendolo, verrà fissato un indice scorrente lungo un arco munito di una scala metrica, come indicato in figura. Per misurare lo spostamento massimo dell'indice per effetto dello sparo, bisognerà studiare un sistema qualunque, dal fine pennello all'estremità dell'indice, al filo trascinato da esso, alla polvere sfiorata da un "baffo", che non offra resistenza al moto.
Uso del pendolo balistico
Per prima cosa bisogna pesare il blocco con precisione. Poi occorre sparare contro il blocco, ad una distanza che eviti l'influenza del gas di sparo (oppure attraverso un diaframma forato) e cercando di colpire il centro del blocco per evitare oscillazioni irregolari. Occorre ricordare che ad ogni sparo successivo al primo, il peso del blocco deve essere aumentato del peso dei precedenti proiettili infissi in esso e che va tenuto conto di perdite di materiale.
Dopo aver sparato si legge quale è stato lo spostamento massimo del pendolo e da esso si ricava la velocità del proiettile. La lettura deve essere fatta con una certa precisione perché, ad esempio, con un pendolo di 130 cm di lunghezza, un errore di lettura di 4 mm (10' di grado), comporta un errore nel calcolo di 5-6 m/sec.
Esempio
Sia da misurare la velocità di un proiettile cal 9 corto e si abbia
Peso del pendolo P , gr. 1500
Peso del proiettile p gr. 6
Lunghezza teorica del pendolo l , m 1,20
Lunghezza totale del pendolo L , cm 130
Arco percorso, cm 40
Applicando l'ultima formula troviamo l'angolo alfa

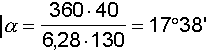
e quindi <

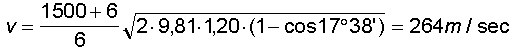
Se si è sparato contro il pendolo da una distanza di metri 1,5, e tenendo conto delle resistenze interne del sistema, si otterrà un valore abbastanza esatto della velocità iniziale aumentando quello sopra trovato dell' 1%.
Si veda la pagina per l'aria compressa