
 |
| back |
Nomenclatura della traiettoria
Traiettoria è la linea curva percorsa nello spazio dal centro
di gravità del proiettile durante il suo movimento.
O Origine della traiettoria; è il centro della
bocca dell'arma (volata) al momento della sparo.
B Punto di arrivo e cioè il bersaglio mirato; è il
punto in cui la linea di sito interseca la traiettoria.
C Punto di caduta; corrisponde all'intersezione del
ramo discendente della traiettoria con la linea di orizzonte
dell'arma. Può coincidere con il punto B se questo si
trova sulla linea di orizzonte.
V Vertice della traiettoria, cioè il punto più alto
che la divide nel ramo ascendente (OV) e nel ramo
discendente (VC).
OP Linea di proiezione; è il prolungamento dell'asse
della canna al momento in cui il proiettile abbandona l'arma;
in termini geometrici è la tangente all'origine della
traiettoria.
OT Linea di tiro. È il prolungamento dell'asse della
canna puntata, prima dello sparo; passerà nella posizione P per effetto del rilevamento.
OB Linea di sito di un punto B della
traiettoria; è la retta che congiunge l'origine della
traiettoria col punto stesso; è cioè la linea retta che
congiunge la volata con il bersaglio.
x Ascissa di un punto B (ad es. OM), è
la distanza del punto B dall'origine misurata
sull'asse orizzontale.
xo Ascissa al vertice (ON).
X Gittata OC, è la distanza tra l'origine e il
punto di caduta.
Y Altezza della traiettoria o ordinata massima o
ordinata al vertice; è il punto della traiettoria più alto
sulla linea dell'orizzonte.
h Ordinata di un punto B (es. BM), è
l'altezza del punto B rispetto all'orizzonte.
BOC Angolo di sito e .
POB Angolo di partenza g .
POC Angolo di proiezione f compreso
fra la linea di proiezione e l'orizzonte .
POT Angolo di rilevamento r ; è l'angolo formato dalla linea di proiezione con la linea
di tiro.
TOB Angolo di elevazione a ; è l'angolo formato dalla linea di tiro con la linea di
sito e corrisponde al cosiddetto alzo.
TOC Angolo di tiro i che
la linea di tiro forma con l'orizzonte.
OCR Angolo di caduta w è
l'angolo acuto formato dalla tangente alla traiettoria nel
punto di caduta con la linea d'orizzonte.
OBL Angolo di arrivo q ;
è l'angolo formato dalla tangente alla traiettoria con la
linea di sito nel punto di arrivo B; non confonderlo con
l'angolo di impatto che è l'angolo formato dalla tangente
alla traiettoria con il terreno nel punto B e dipende perciò
dall'andamento del terreno.
La balistica è quel ramo della fisica che studia il moto dei
proiettili che avviene all'interno della canna dell'arma
(balistica interna), nello spazio esterno (balistica esterna) e,
infine, entro il bersaglio colpito (balistica terminale).
Nello spazio esterno il proiettile percorre una traiettoria
che è il risultato di tre distinte forze (qui trascurando dati
che interessano solo per missili o proiettili a lunghissima
gittata): l'impulso iniziale che gli imprime un moto uniforme e
rettilineo, la resistenza dell'aria che si oppone ad esso in
senso contrario, la forza di gravità che tende a far cadere il
proiettile verso il suolo con moto uniformemente accelerato.
La resistenza dell'aria assume un ruolo rilevante per
proiettili veloci e quindi, per proiettili molto lenti
(artiglierie antiche, frecce, sassi) può essere pressoché
trascurata (per un mortaio ottocentesco la differenza rispetto
alla traiettoria nel vuoto era soltanto del 10%).
Il calcolo del moto di un proiettile nel vuoto è alquanto
semplice.
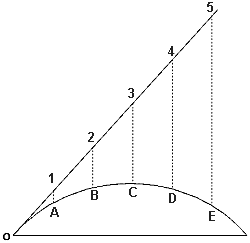
ricaviamo che dopo un secondo (t) il proiettile sarà caduto dello spazio s fino al punto A, dopo due secondi fino al punto B, dopo tre secondi fino al punto C, e così via. Collegando tutti i punti A, B, C, ... si ottiene la traiettoria percorsa dal proiettile. Essa è rappresentata da una parabola simmetrica in cui l'angolo di partenza è eguale all'angolo di caduta, la velocità iniziale è eguale alla velocità finale e il vertice la divide in due rami simmetrici. Essa può essere calcolata conoscendo solo i parametri V (velocità iniziale) e (angolo di partenza).
La gittata X si ottiene dalla formula
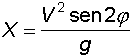
da cui si deduce che la gittata massima si ottiene con un angolo di partenza di 45° quando il valore del seno dell'angolo è eguale ad uno; il che significa, ad esempio, che, trascurando la resistenza dell'aria, una freccia lanciata alla velocità di 100 m/s arriva al massimo alla distanza di 1019 metri.
Il tempo di volo del proiettile fino ad una data distanza è dato da
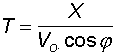
Quando il moto del proiettile invece che nel vuoto avviene
nell'aria, assume importanza fondamentale la forza ritardatrice
dovuta alla resistenza del mezzo. Un proiettile cal. 9 Para con V0 = 330 m/s, che nel vuoto avrebbe una gittata
massima di 11.100 metri, nell'aria ha una gittata massima di
circa 1500 metri; un proiettile di moschetto è assoggettato ad
una forza ritardatrice che riduce la sua velocità finale ad 1/6
di quella iniziale. La traiettoria percorsa non è quindi
simmetrica, ma ad un ramo ascendente più lungo, segue un ramo
discendente più curvo e corto così che l'angolo di caduta è
maggiore dell'angolo di partenza.
In linea generale la traiettoria è tanto più curva quanto
più lento è il proiettile per il fatto che la forza di gravità
agisce più a lungo. Il peso del proiettile, a parità di
velocità, non incide sulla maggiore o minore curvatura della
traiettoria ed in teoria, a parità di forma e di velocità
iniziale, il maggior peso rende più tesa la traiettoria, sia
pure in misura trascurabile alle distanze venatorie (infatti se
il proiettile pesa di più, a parità di calibro aumenta la sua
lunghezza e la densità sezionale e migliora quindi il suo
comportamento balistico). In pratica però, specie nelle armi
leggere, il proiettile più pesante viene sparato a velocità
inferiori rispetto ad un proiettile leggero, con la conseguenza
che la sua traiettoria sarà meno tesa.
Il calcolo della resistenza dell'aria e della relativa
ritardazione, è semplice per velocità inferiori ai 200 m/s per
cui si può assumere che la resistenza vari con tasso inferiore
al quadrato della velocità, ma diventa difficile a velocità
superiori in cui essa varia con un tasso assai maggiore, con
un'impennata per velocità prossime al muro del suono, ed è
influenzata da numerosi fattori, quali la densità dell'aria alle
diverse altezze raggiunte (e con il variare della densità varia
la velocità del suono e quindi la ritardazione), i moti di
oscillazione e di precessione del proiettile durante il volo,
ecc. Ovviamente poi la resistenza varia a seconda della forma
più o meno aerodinamica del proiettile e risultati precisi si
possono ottenere solo su basi sperimentali, redigendo per ogni
proiettile apposite tavole di tiro, cosa che fa ogni esercito per
le sue artiglierie.
Per calcoli di una certa approssimazione, si sono però
studiate delle leggi generali di resistenza dell'aria, più che
sufficienti per scopi pratici: dopo aver tracciato
sperimentalmente le curve della resistenza dell'aria riferite a
diversi tipi di proiettile, si è ricavata una curva intermedia
teorica o riferita ad un proiettile tipo; da questa, introducendo
un coefficiente (coefficiente balistico, ricavato dal suo calibro
e dal suo peso, integrato dal coefficiente di forma "i",
ricavato dalla forma del proiettile), che indicano il rapporto
tra proiettile tipo e proiettile in esame, si risale ai valori
reali.
La formula per il coeff. balistico è data da
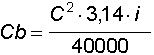
in cui il calibro C è espresso in millimetri. Il valore di i è il dato più difficile da calcolare anche perché varia in
relazione alla velocità; in via di prima approssimazione si può
ritenere che esso vari da 0,44 per proiettili appuntiti, tipo
quelli per moschetto militare, a 1 - 1,2 per proiettili da
pistola o rivoltella, fino a 3 - 4 per proiettili cilindrici (wad
cutter).
In tempi più recenti in luogo del concetto di coefficiente
balistico si è introdotto quello di coefficiente aerodinamico Cx che per i proiettili varia da 0,1 a 0,5. Anch'esso non è
costante, ma varia in relazione alla velocità espressa in Mach.
Il calcolo di una traiettoria di un proiettile moderno è
comunque estremamente complicato e richiede l'impiego di
matematiche superiori. Si può ovviare con l'impiego di metodi
grafici o di tavole di ritardazione già compilate, ma si tratta
comunque di attività laboriose. Attualmente sono in commercio
numerosi programmi di balistica per computer, limitati però a
traiettorie di pratico impiego, di poche centinaia di metri e
tese, in cui l'angolo di proiezione non supera i 5°.
La gittata massima
Non è possibile indicare una semplice formula matematica che
consenta di calcolare con buona approssimazione la gittata
massima di un proiettile, cioè la massima distanza a cui il
proiettile può arrivare nella migliore delle ipotesi.
In via molto approssimata può usarsi la mia formula in cui il risultato è espresso in chiolometri:
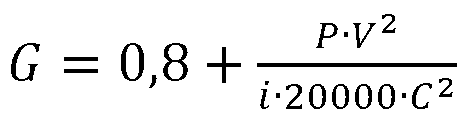
in cui P è il peso in grammi, V la velocità in m/s, C il
calibro in millimetri ed i il fattore di forma. Essa è valida
principalmente per proiettili oltre i 10 mm.
Un'altra formula approssimativa richiede la conoscenza della velocità iniziale e
della velocità residua ad una data distanza y, che qui si assume = a 100 metri.
La gittata massima sarà data da
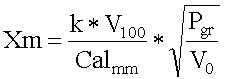
| Calibro | Velocità m/s | Gittata in m. |
| 4,5 mm aria compressa | 120/165 | 100/150 |
| 4,5 mm aria compressa | 200/250 | 200/300 |
| 6/9 mm Flobert | 225 | 700 |
| .22 corto | 260 | 1000 |
| .22 Long Rifle | 350 | 1370 |
| .22 Long Rifle HS | 370 | 1500 |
| .22 Winch. Magnum | 610 | 1800 |
| 243 Winch. | 1070 | 3200 |
| 6,35 mm | 220 | 800 |
| 7,65 mm | 285 | 1300 |
| 9 mm corto | 285 | 1300 |
| 9 mm Para | 350 | 1700 |
| .45 ACP | 300 | 1620 |
| 30 M1Carb. | 600 | 2000 |
| 7x70 mm | 830 | 3500 |
| 8x57 mm JS | 830 | 3500 |
| 6,5x57 mm | 1020 | 4000 |
| 7x57 mm | 850 | 4500 |
| 6,5x68 mm | 1150 | 5000 |
Siccome la mia formula non è il massimo per precisione, riporto un utile nomogramma
che consente di calcolare i valori per la gittata massima. Non va bene per piccoli proiettili,
perché il valore di ingresso nella tavola è troppo piccolo.
Nomogramma per la gittata massima, tempo di volo e angolo
di proiezione
Il seguente nomogramma, tratto dal manuale della Rheinmetall, consente di
calcolare graficamente e con buona approssimazione la gittata massima in
relazione a calibro e peso del proiettile ed alla velocità iniziale.
Esso è basato su di un proiettile teorico (legge di resistenza della Rheinmetall)
con Cx= 2 alle basse velocità, e Cx = 4 alle velocità supersoniche.
In rapporto alle leggi di resistenza su cui si basano le tavole usuali (Siacci,
Saengewald) si ha i=1 fino alla velocità di 320 m/s; da 360 m/s in poi si può
assumere i=1,5
In relazione alla gittata massima individuata si può leggere poi e l'angolo di
proiezione che consente di ottenerla e il relativo tempo di volo.
Facendo un esempio pratico, si procederà così:
Calibro 26 mm (raggio 13 mm)
Peso 440 gr.
Vo 600 ms
Occorre trovare il valore da 0 a 40 con cui entrare nella tavola ed esso sarà dato
dal fattore di forma i diviso per la densità sezionale Q (kg/mq); se il
proiettile ha forma standard i=1 il valore ricercato è dato dal valore
reciproco di Q. La superficie della sezione sarà data da 3,14 x 13² = 530 mmq
e quindi il valore ricercato, moltiplicato per 10 al fine di eliminare inutili
virgole, sarà dato da
Il tiro verticale
Un proiettile sparato verticalmente verso l'alto raggiunge
un'altezza pari a circa il 70% della gittata massima. Nel
ricadere verso il basso il proiettile aumenta progressivamente la
sua velocità, come qualsiasi corpo in caduta libera, finché la
ritardazione dovuta alla resistenza dell'aria non eguaglia la
forza di gravità; da quel momento la velocità del proiettile
rimane costante (velocità limite). Se il proiettile è stato
sparato proprio verticalmente, e quindi non compie alcuna
traiettoria, ricadrà con il fondo piatto verso il suolo e
offrirà una grande resistenza all'aria così che la sua
velocità finale sarà di circa 30-50 m/s, non idonea a provocare
lesioni ad una persona. Se è stato sparato con un piccolo angolo
rispetto alla verticale, si capovolge e ricade con la punta in
avanti; un proiettile di pistola può raggiungere i 100 m/s e uno
di moschetto i 180 m/s, del tutto idonei a provocare gravi
lesioni (si consideri che quest'ultimo può ancora penetrare per
30-40 cm nel corpo umano).
Il proiettile ricade in genere nel raggio di una decina di
metri dal tiratore, ma può essere spostato dal vento anche di
200 metri. Il tempo che un proiettile di moschetto impiega a
ricadere è di circa 30 secondi se con la punta in avanti e di
oltre il doppio se è capovolto, il che può dar luogo a ferite
apparentemente inspiegabili.
L'influenza del vento
L'influenza del vento che spira a favore o contro il
proiettile può essere trascurato per le normali distanze
d'impiego delle armi leggere. Ha invece un'influenza
significativa quando soffia trasversalmente alla traiettoria. Il
calcolo può essere solo molto approssimativo poiché il vento
non è costante, ma soffia a raffiche e non ha velocità costante
poiché essa varia in relazione ad
ostacoli ed alla distanza dal suolo. Supposto comunque che si
possa ipotizzare una certa velocità e che il vento soffi
perpendicolarmente alla traiettoria, trova applicazione la
formula di Didion la quale ci dice che lo spostamento D, in
metri, del proiettile dal punto mirato, ad una data distanza X,
è dato dalla velocità del vento W moltiplicata per la
differenza tra tempo di volo nell'aria T e tempo di volo nel
vuoto per il valore di X considerato, e cioè
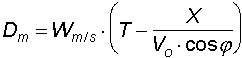
A titolo di esempio si consideri che un vento di 10 m/s (vento sensibile che alza polvere e piega alberelli), sposta un proiettile di fucile militare, su di un bersaglio posto a 300 metri, di circa 50 cm.
Se il vento non è perpendicolare ma forma un certo angolo "a " con la traiettoria, il risultato D dovrà essere moltiplicato per il valore di cos2a .
Densità dell'aria
La densità dell'aria determina la resistenza al moto del
proiettile e, come si è visto, entra in tutte le formule
concernenti la resistenza dell'aria Essa varia in relazione alla
temperatura ed alla pressione atmosferica e, in misura minore in
relazione all'umidità.
Con formula molto approssimata, la densità dell'aria, che viene
essere assunta pari a 1,225 kg/mc nell'atmosfera standard al
livello del mare ed alla temperatura di 15 gradi, può essere
calcolata con la seguente formula, nota la temperatura e la
pressione atmosferica in millimetri di mercurio,
![]()
Ricordo che la pressione in mm di mercurio si ottiene moltiplicando la pressione in millibar per 0,75 e che la temperatura, in linea di massima, diminuisce di 0,65 gradi quando si sale di 100 metri.
Quando non si conosce la pressione atmosferica ma solo l'altitudine H del luogo ove si sviluppa la traiettoria del proiettile, la formula di cui sopra diventa
![]()
Per gli usi normali di un'arma nelle nostre regioni, la
densità dell'aria può però essere trascurata dallo sparatore;
in genere la diminuzione di densità dovuta al crescere
dell'altitudine, viene compensata dalla diminuzione di
temperatura e, comunque, il fatto di sparare in un'atmosfera meno
densa, come avviene in alta montagna, comporta un miglioramento
della traiettoria che sarà più tesa.
La derivazione del proiettile
Una canna rigata ha al suo interno le cosiddette righe che, come la filettatura di
di una vite, si sviluppano con un certo passo (tratto di canna in cui il proiettile
compie una intera rotazione su se stesso)e con un certo angolo di rigatura
(inclinazione della rigatura rispetto all'asse longitudinale della canna); il
rapporto che lega l'angolo di rigatura con il passo è dato dalla formula
![]()
Nr.giri al secondo = V /passo in cm
in cui V è la velocità alla bocca in ms.![]()
in cui X è la gittata in metri e l'angolo è quello di proiezione.Il risultato D è espresso in metri.
Un'altra formula, ancora più approssimata ci dice che la derivazione, in metri, è pari a 0,11 moltiplicato per il tempo di volo al quadrato (il valore 0,11 è un valore medio che andrebbe calcolato per ogni proiettile).
Raccolta di formule approssimate
Qui di seguito riporto alcune formule molto approssimative che
consentono di ottenere valori orientativi partendo da altri
valori noti.
1) Ordinata per una distanza x non
troppo grande
![]()
2) Angolo di proiezione nota la gittata massima
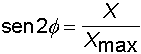
3) Angolo di proiezione noto il tempo di volo
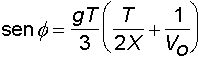
4) Ordinata massima
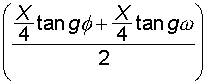
5) Ordinata massima noto il tempo di volo (formula di Haupt)
![]()
6) Ordinata massima noti gittata e angoli di partenza e caduta
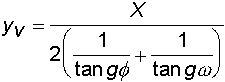
7) Ascissa del vertice nota la gittata
![]()
8) Ascissa del vertice nota la gittata e la velocità iniziale
![]()
9) Ascissa del vertice noti la gittata, l'ordinata e l'angolo di partenza
![]()
10) Velocità del proiettile al vertice
![]()
11)Angolo di caduta noti tempo di volo, gittata e velocità di caduta

12) Angolo di caduta noti gittata, ordinata e angolo di partenza
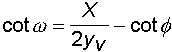
13) Velocità di caduta
![]()
Tavola di raffronto tra i valori calcolati con le formule approssimate e i valori effettivi

| Sitemap: in Italiano | auf Deutsch | in English | |
| http://www.earmi.it - Enciclopedia delle armi © 1997 - 2003 |